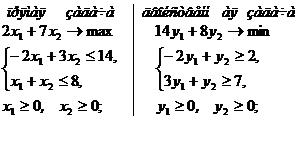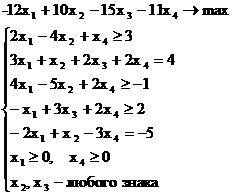Понятие двойственности. Построение пары взаимно двойственных задач

С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется прямой или исходной. Многие задачи линейного программирования первоначально ставятся в виде исходных или двойственных задач, поэтому говорят о паре взаимно двойственных задач линейного программирования. Пара симметричных двойственных задач ЛП имеет следующий вид:

Рассмотренная пара взаимно двойственных задач может быть экономически интерпретирована, например, так.

Прямая задача: сколько и какой продукции х_j надо произвести, чтобы при заданных стоимостях единицы продукции c_j , объёмах имеющихся ресурсов b_i и нормах расходов а_ij максимизировать выпуск продукции в стоимостном выражении?

Двойственная задача: какова должна быть оценка единицы каждого из ресурсов y_i , чтобы при заданных b_i, c_j, a_ij минимизировать общую оценку затрат на все ресурсы?

Пример 1.

Правило построения двойственной задачи в несимметричной форме:

1. упорядочивается запись исходной задачи, т.е. если целевая функция задачи максимизируется, то ограничения неравенства должны быть вида ≤ , если минимизируется — то вида ≥. Выполнение этих условий достигается умножением соответствующих ограничений на (-1);

2. Если прямая задача решается на максимум, то двойственная на минимум;

3. В задаче на максимум ограничения - неравенства имеют смысл ≤, а в задаче минимизации - смысл ≥;

4. Каждому ограничению прямой задачи соответствует переменная двойственной задачи, и наоборот, каждому ограничению двойственной задачи соответствует переменная прямой задачи;

5. Матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием;

6. Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи, и наоборот;

7. Если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, если же нет, то как ограничение-равенство.

8. Если какое-либо ограничение прямой задачи записывается как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.

Пример 2. Пусть имеем задачу ЛП в произвольной несимметричной форме. Построить ей двойственную:

РешениеПрежде всего ограничения типа ≥ умножением на -1 сведём к ограничениям  ≤. Получим

Пользуясь правилом построения двойственной задачи в несимметричной форме получим следующую модель задачи: