
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Максимизация целевой функции FДля нахождения точки, в которой функция F достигнет своего максимального значения, необходимо перемещать прямую уровня по направлению вектора а до пересечения этой прямой с граничной точкой области допустимых решений. На нашем рисунке - это точка В. Найдем координаты точки В. Данная точка расположена на пересечении двух прямых (1') и (2'), поэтому, чтобы найти ее координаты необходимо решить следующую систему уравнений:
Из второго уравнения выразим х1.
И подставим полученное значение в первое уравнение.
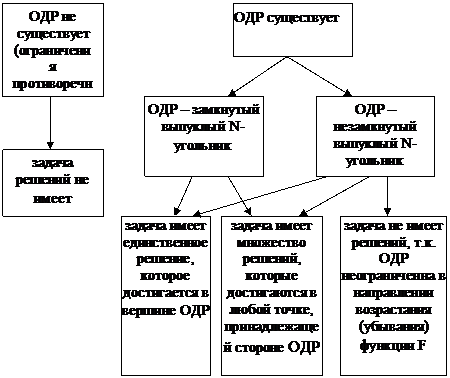
(300; 200) - точка, соответствующая оптимальному решению задачи, следовательно, максимальная прибыль составляет 2*300+4*200 = 1400 дол. в неделю. Значит, чтобы получить максимальную прибыль, фирме необходимо выпускать в неделю триста полок модели А и двести полок модели В. 3.3.4 Алгоритм решения задачи двумерного линейного программирования графическим методом. 1. Строим область допустимых решений функции F. Для этого в ограничениях знаки неравенства заменяем знаками равенства и строим полученные прямые. Затем определяем те полуплоскости, которые соответствуют данным ограничениям и получаем область допустимых решений, лежащую на пересечении всех полуплоскостей. 2. Строим прямую уровня Для этого берем произвольную точку М, принадлежащую области допустимых решений функции F и, подставив координаты этой точки в функцию, получаем прямую уровня. Затем от выбранной точки М, откладываем вектор а, координаты которого - это коэффициенты при целевой функции F. 3. Максимизируем (минимизируем) целевую функцию F. Для максимизации (минимизации) функции F передвигаем прямую уровня по направлению (в обратном направлении относительно) вектора и до пересечению с граничной точкой области допустимых решений. Полученная точка является оптимальным решением, в котором функция достигает свой максимум (минимум). Находим координаты этой точки и подставляем их в функцию F.  При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР - область допустимых решений)
Симплекс-метод. Существует универсальный способ решения задач ЛП, называемый симплекс-методом. Идея симплекс-метода. Сначала надо найти некоторую (начальную) вершину многогранника допустимых решений (начальный опорный план). Затем надо проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
рис.4.1
Построение начального опорного плана.
Рассмотрим три случая. 1-й случай. Пусть в системе ограничений имеется единичный неотрицательный базис. Например, она имеет вид
Говорят, что ограничение канонической ЗЛП имеет предпочтительный вид, если при неотрицательности его правой части (bi ³ 0) левая часть содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения – с коэффициентом равным нулю. Если каждое ограничение канонической ЗЛП имеет предпочтительный вид, т. е. система ограничений приведена к единичному неотрицательному базису, то начальный опорный план строится весьма просто. Предпочтительные переменные выбираются в качестве базисных, а все остальные – свободные. Свободные переменные приравниваются нулю, а базисные переменные – свободным членам. Пример.Найти начальный опорный план ЗЛП
РешениеВ первом ограничении предпочтительной переменной является х4, во втором – х2. Система приведена к положительному единичному базису. Свободные переменные х1 и х3 приравниваются нулю. Получим невырожденный начальный опорный план: х0 = (0; 3; 0; 2); Z(x0) = 0. 2-й случай. Пусть система ограничений имеет вид
Сведем задачу к каноническому виду, добавив к левым частям системы ограничений дополнительные переменные хn+i ³ 0 (i=1…m). Получим систему ограничений
эквивалентную исходной и имеющую предпочтительный вид. Отсюда получаем начальный опорный план:
В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю:
Пример. Найти начальный опорный план ЗЛП
РешениеПриведем задачу к каноническому виду:
Система ограничений имеет предпочтительный вид. Начальный опорный план
2-й случай. Пусть система ограничений имеет вид
Перейдем к каноническому виду путем введения дополнительных переменных хn+i ³ 0 (i=1…m):
Теперь система ограничений, вообще говоря, не имеет предпочтительного вида. В этом случае вводят искусственный базис путем перехода к М- задаче:
где в целевой функции знак «-» относится к задаче максимизации. Если некоторые из уравнений исходной системы ограничений имеют предпочтительный вид, то в них не вводят искусственные переменные. Начальный опорный план М – задачи имеет вид
Между оптимальными планами исходной задачи и М – задачи имеется следующая связь: если в оптимальной задачи и М – задачи все искусственные переменные wi* равны нулю, то значения оставшихся координат плана х* дадут оптимальный план исходной задачи.
Пример. Найти начальный опорный план задачи
Решение. Вводя дополнительные х5, х6, х7 и искусственные переменные, переходим к задаче в каноническом виде и к М – задаче:
Ее начальный опорный план
Симплексные таблицы
Приведя модель ЗЛП к предпочтительному виду, ее заносят в так называемую симплексную таблицу. Таблица 4.1
Рабочая часть таблицы, начиная с 3-го столбца и 3-й строки, содержит элементы расширенной матрицы, над которыми будут производиться преобразования с целью получения оптимального плана. В последней строке (zj-cj) таблицы записано «нулевое» уравнение (целевая функция Z). Эта строка называется уравнение индексной или строкой оценок. В столбец БП занесены базисные (предпочтительные) переменные. Столбец сБ содержит коэффициенты целевой функции, стоящие при базисных переменных. Столбец А0 содержит свободные члены bi ³ 0 системы ограничений. Сверху над рабочей частью таблицы указаны все переменные и коэффициенты целевой функции cj. Остановимся на заполнении индексной строки zj-cj. Здесь расположены значение целевой функции для начального опорного плана х0 ,т. е. z(х0) = D0 = сБ × A0, и оценки индексной строки Dj = сБ × Aj – cj.
Проиллюстрируем процесс заполнения таблицы на примере следующей задачи: Пример.
Решение Введя дополнительные переменные х4, х5 и х6, придем к канонической форме: .
Заносим условия задачи в симплексную таблицу Таблица 4.2
Индексная строка zj-cj заполнена по известным формулам D0 = сБ × A0, Dj = сБ × Aj – cj: D0 = 0 × 720 + 0 × 384 + 0 × 360 = 0 D1 = 0 × 18 + 0 × 6 + 0 × 5 – 18 = -18 D2 = 0 × 15 + 0 × 4 + 0 × 3 - 20 = -20 D3 = 0 × 12 + 0 × 8 + 0 × 12 - 32 = -32 D4 = 0 × 1 + 0 × 0 + 0 × 0 - 0 = 0 D5 = 0 × 0 + 0 × 1 + 0 × 0 - 0 = 0 D6 = 0 × 0 + 0 × 0 + 0 × 1 - 0 = 0. Приравнивая х1, х2 и х3 нулю, находим х4 = 720, х5 = 384, х6 = 360 и тем самым начальный опорный план Признак оптимальности опорного плана задачи максимизации: если для некоторого опорного плана все оценки Dj неотрицательны, то такой план оптимален; если же исходная задача на минимум и Dj неположительны, то такой план оптимален. Так, содержащийся в табл. опорный план не является оптимальным, поскольку D1 = -18, D2 = -20, D3 = -32. Рассмотрим переход к нехудшему опорному плану на примере ЗЛП на максимум. Приведем ее к каноническому виду и занесем в симплексную таблицу. Если все Dj ³ 0, то начальный опорный план х0 оптимален. Если же существуют Dj < 0, то план неоптимален, при определенных условиях его можно улучшить. Среди отрицательных оценок находят максимальную по абсолютной величине:
Столбец j0 называется разрешающим. Если задача решается на минимум, то разрешающий столбец выбирается из условия
Переменную
(они называются симплексными). Среди симплексных отношений определяют наименьшее, т. е.
Оно и укажет строку, в которой содержится исключаемая из базиса переменная 1) элементы строки i0 новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, деленным на разрешающий элемент; 2) все элементы столбца j0 новой таблицы равны нулю, за исключением 3) чтобы получить все остальные элементы (включая элементы индексной строки) новой таблицы, надо из соответствующего элемента прежней таблицы вычесть произведение элемента разрешающей строки на элемент разрешающего столбца, разделенное на разрешающий элемент.
Для контроля вычислений элементов индексной строки применяют формулы: D0 = сБ × A0, Dj = сБ × Aj – cj:
Альтернативный оптимум (признак бесконечности множества оптимальных планов): если в индексной строке последней симплексной таблицы (содержащей оптимальный план) имеется хотя бы одна нулевая оценка, соответствующая свободной переменной (небазисные переменные), то задача ЛП имеет бесконечное множество оптимальных планов. Признак неограниченности целевой функции: если в разрешающем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена. Признак несовместимости системы ограничений: если в оптимальном плане М- задачи не все искусственные переменные равны нулю, то система ограничений исходной задачи несовместна.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 424. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||









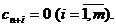



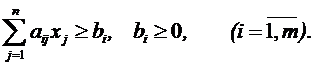
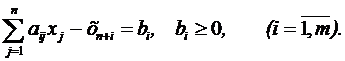



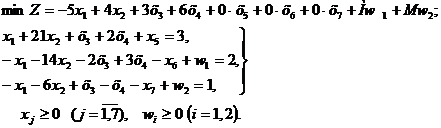



 В столбце A0 индексной строки получено значение D0 = 0 целевой функции, соответствующее плану х0.
В столбце A0 индексной строки получено значение D0 = 0 целевой функции, соответствующее плану х0.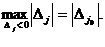

 , соответствующую разрешающему столбцу, следует ввести в базис. Для определения переменной, выводимой из базиса, находят отношения
, соответствующую разрешающему столбцу, следует ввести в базис. Для определения переменной, выводимой из базиса, находят отношения

