
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модифицированный алгоритм ДийкстрыДля решения задачи нахождения кратчайшего пути в сети с отрицательными весами служит следующий алгоритм. 1. На шаге 2 перерасчет величин l(u) производится для всех вершин u, а не только для неокрашенных вершин. 2. Если для некоторой вершины u величина l(u) уменьшается, то с этой вершины и с инцидентной ей окрашенной дуги окраска снимается. 3. Процедура продолжается до тех пор, пока все вершины не окажутся окрашенными и ни одно из чисел l(u) больше не меняется.
Пример. Рассмотрим пример, приведенный в замечании 3. Шаг 1. l(s) = 0, l(a) = l(t) = ∞. Шаг 2. Пересчитаем метки l(u). l(a) = min {l(a), l(s) + l(s, a)} = min {∞, 0+2} = 2, l(t) = min {l(t), l(s) + l(s, t)} = min {∞, 0+1} = 1, Окрашиваем вершину t и дугу (s, t) (рис. 1.11).
Рис. 1.11
Вершина a не окрашена, поэтому пересчитываем метки l(ν) для всех ν. Так как из вершины t дуг не выходит, то метка не меняется. Выбираем минимум по неокрашенным вершинам, в результате чего окрашиваем вершину a и дугу (s, a) (рис.1.12).
Рис. 1.12
Снова производим перерасчет. l(t) = min {l(t), l(a) + l(a, t)} = min {1, 2-1} = 0, l(s) = min {0, 2+∞} = 0. Для вершины t метка l(t) уменьшилась, поэтому снимаем с вершины t и дуги (s, t) окраску (рис.1.13)
Рис. 1.13 Пересчитываем из вершины a метки, в результате чего окрашиваем дугу (a, t) и вершину t (рис. 1.14).
Рис. 1.14 Снова пересчитываем метки. Они не меняются и все вершины окрашены. Алгоритм завершен, и кратчайший путь построен: (s, t) ={(s, a), (a, t)}.
Замечание 4.Модифицированный алгоритм Дийкстры не решает рассматриваемую задачу при наличии в исходном графе контура, имеющего отрицательную длину. Действительно, проходя вдоль данного контура неограниченное число раз, можно сделать длину пути сколь угодно малой по величине. 
Нахождение кратчайших цепей между всеми парами узлов в сети
Рассмотрим сеть, каждой дуге (u, ν) которой поставлено в соответствие действительное число l(u, ν), называемое длиной дуги. В зависимости от конкретного приложения, это число может быть мерой физического расстояния, времени, стоимости или другого параметра. Длиной цепи называется сумма длин, взятая по всем дугам этой цепи. Рассматривается задача нахождения кратчайших цепей между всеми парами узлов в сети. Предполагается, что сумма длин дуг по любому направленному циклу должна быть неотрицательна (иначе понятие кратчайшей цепи теряет смысл).
Алгоритм Флойда (Floyd R. W.) Шаг 0. Пусть N = {1, 2, …n} — множество узлов сети. На j-й итерации работы алгоритма будем строить матрицу расстояний Lp, элемент которой Алгоритм начинает работу с
и
После построения матриц Шаг 1. Пусть матрицы Шаг 2. Построим матрицы Если Если Шаг 3. Элемент матрицы Замечание. 1. Если 2. Если
Пример. В данной сети (рис. 1.15) найти кратчайшую цепь между всеми парами узлов в сети.
Рис. 1.15 Решение: Составляются матрицы
Итерация 1. Узел p=1 определяется как базовый. Выделяем в матрице
Применяя к этим элементам алгоритм Флойда, получаем следующие матрицы:
Итерация 2. Определяем узел p=2 как базовый. Выделяем вторую строку и второй столбец в матрице
Используя алгоритм Флойда, получаем матрицы:
Далее аналогично действуя, получаем:
Длина кратчайшей цепи, например, из узла 5 в узел 4 равна
Замечание. Алгоритм Флойда может быть использован для нахождения в графе циклов отрицательной длины. Если на k-й итерации в матрице
Задача об «узких» местах Определение«Узким» местом цепи называется кратчайшая из входящих в него дуг. Задача об узких местах — это задача поиска такого пути между двумя вершинами, в котором длина кратчайшей дуги максимальна. Пример.Рассмотрим транспортную сеть, включающую мосты. Будем предполагать, что при превышении грузоподъемности некоторого моста, последний разрушается. Необходимо определить максимальный вес груза, который может быть транспортирован в рассматриваемой сети из пункта А в пункт В, без повышения грузоподъемности находящихся на маршруте движения мостов. Если поставить в соответствие мостам дуги графа и задать длины дуг равными соответствующим ограничениям на нагрузку моста, то задача сводится к задаче поиска такого пути между узлами А и В, в котором длина кратчайшей дуги максимальна. Для решения такого рода задач можно использовать модификацию алгоритма Флойда.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 405. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




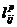 равен кратчайшей (i, j)- цепи, промежуточными узлами в которой могут быть лишь узлы из множества {1, 2, … , p}; и справочную матрицу Sp, каждый элемент
равен кратчайшей (i, j)- цепи, промежуточными узлами в которой могут быть лишь узлы из множества {1, 2, … , p}; и справочную матрицу Sp, каждый элемент  которой указывает на первый после узла i узел в такой цепи.
которой указывает на первый после узла i узел в такой цепи. , где
, где

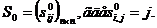
 и
и  для каждого p = 1,2,…,n, используя для вычислений элементы матриц, полученных на предыдущих итерациях, необходимо выполнить следующую процедуру:
для каждого p = 1,2,…,n, используя для вычислений элементы матриц, полученных на предыдущих итерациях, необходимо выполнить следующую процедуру: и
и 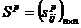 найдены. Выделим элементы p-й строки и p-го столбца матрицы
найдены. Выделим элементы p-й строки и p-го столбца матрицы  . Назовем эти множества элементов базовой строкой и базовым столбцом соответственно.
. Назовем эти множества элементов базовой строкой и базовым столбцом соответственно. и
и  исходя из следующего правила: для
исходя из следующего правила: для 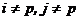 .
.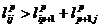 , то
, то  и
и  .
.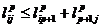 , то
, то  и
и  .
.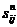 есть узел, стоящий после узла i в этой цепи.
есть узел, стоящий после узла i в этой цепи. , т.е. i-й элемент базового столбца равен
, т.е. i-й элемент базового столбца равен  , то для i-й строки шаг 2 выполнять не нужно.
, то для i-й строки шаг 2 выполнять не нужно. , т.е. j-й элемент базовой строки равен
, т.е. j-й элемент базовой строки равен 
 .
.
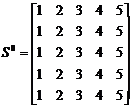
 , следует исследовать лишь элементы матрицы
, следует исследовать лишь элементы матрицы  , показанные ниже
, показанные ниже

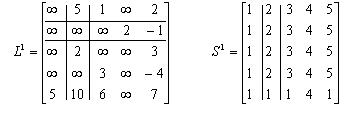
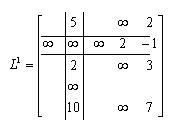





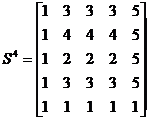


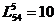 . Для определения узлов соответствующей цепи, обратимся к матрице
. Для определения узлов соответствующей цепи, обратимся к матрице 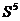 . Нетрудно заметить, что
. Нетрудно заметить, что 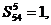


 . Следовательно, кратчайшая цепь из узла 5 в узел 4 определяется последовательностью узлов 5"1"3"2"4.
. Следовательно, кратчайшая цепь из узла 5 в узел 4 определяется последовательностью узлов 5"1"3"2"4. на диагонали появилось отрицательное число
на диагонали появилось отрицательное число  , то это означает, что в графе существует цикл отрицательной длины. Найти цикл можно, используя справочную матрицу Sk.
, то это означает, что в графе существует цикл отрицательной длины. Найти цикл можно, используя справочную матрицу Sk.