Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нахождение кратчайших путей между двумя заданными вершинами. Алгоритм ДийкстрыСтр 1 из 19Следующая ⇒ СИСТЕМНЫЙ АНАЛИЗ И МОДЕЛИРОВАНИЕ
Методическое пособие
МИНСК 2009 Министерство образования республики беларусь Учреждение образования «Минский государственный высший радиотехнический колледж»
СИСТЕМНЫЙ АНАЛИЗ И МОДЕЛИРОВАНИЕ
Методическое пособие для студентов специальности 1-08 01 01 07 «Профессиональное обучение. (Информатика)» для учащихся специальности 2-40 01 01 «Программное обеспечение информационных технологий»
МИНСК 2009
Рекомендовано к изданию кафедрой информатики и Научно-методическим советом Учреждения образования «Минский государственный высший радиотехнический колледж»
С о с т а в и т е л и Г. Н. Соловей, ассистент кафедры информатики С. Н. Кудина, ассистент кафедры информатики И. Г. Смолер, ассистент кафедры информатики
Р е ц е н з е н т Ю. А. Скудняков, зав. кафедрой информатики МГВРК, канд. техн. наук, доцент
Системный анализ и моделирование : методическое пособие для студентов специальности 1-08 01 01 07 «Профессиональное обучение. (Информатика)» для учащихся специальности 2-40 01 01 «Программное обеспечение информационных технологий» / сост. Г. Н. Соловей, С. Н. Кудина, И. Г. Смолер – Мн. : МГВРК, 2009. – с.
Цель пособия – обеспечить учащихся и студентов необходимым теоретическим и практическим материалом, позволяющим самостоятельно решать задачи с использованием основных алгоритмов курса «Системный анализ и моделирование» Предназначено для учащихся, студентов и преподавателей колледжа.
Предисловие Учебная дисциплина «Системный анализ и моделирование» занимается исследованием, моделированием сложных систем различной природы: технических, экономических, экологических. При этом проводится исследование, как отдельных элементов системы, так и всей системы в целом.  Обязательным элементом при проведении современных системных исследований является использование вычислительной техники. Результатом системных исследований является принятие конкретных решений, обеспечивающих оптимальное функционирование системы, выдача рекомендаций для эффективного использования полученных результатов на практике. Данное учебное пособие предназначено для учащихся и студентов ……специальностей, специализирующихся в области разработки и использования информационных технологий для решения широкого круга экономических задач, в том числе – связанных с моделированием экономических процессов. В пособии представлены разделы, посвященные построению математических моделей для решения ряда экономических задач. В результате изучения данного пособия учащиеся истуденты приобретают навыки построения экономико-математических моделей, их использования для объяснения поведения исследуемых экономических показателей, и их взаимосвязи. В учебном пособии представлены следующие разделы одноименной учебной дисциплины: теория графов, линейное программирование, теория двойственности, транспортная задача, дискретное программирование, динамическое программирование, матричные игры. Данное пособие содержит материал для подготовки и проведения практических работ. Для учащихся и студентов, стремящихся достичь высокого профессионального уровня в области программирования, предлагается лабораторный практикум, реализация задач которого возможна на языках программирования высокого уровня: Pascal, Delphi, Си.
Теория графов Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение, как в программировании, так и в моделировании. Это связано с тем, что теория графов предоставляет удобный язык для описания программных моделей. Логически упорядоченная система специальных терминов и обозначений теории графов позволяет просто и доступно описывать сложные задачи. Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач. Например, задача о Кенигсбергских мостах (Эйлер, 1736 г.), задача о трех домах и трех колодцах (К. Куратовский, 1930 г.), задача о четырех красках (Апель и Хекен, 1976 г.). Решение некоторых задач «программным путем» является прецедентом, породившим бурную дискуссию, которая до настоящего времени еще незакончена. 1.1 Остовные деревья минимального веса. Алгоритмы Прим, Краскал.
Определение. Пусть Постановка задачи. Имеется связный граф, каждому ребру которого поставлено в соответствие неотрицательное число, называемое весом ребра. Требуется найти остовное дерево минимального веса (вес дерева равен сумме весов ребер, входящих в него). Алгоритм Прим Шаг 1. На первом шаге в качестве подграфа На каждом последующем шаге к уже построенному графу добавляется одно ребро. Шаг k.Если граф 1) l инцидентно какому-либо ребру графа 2) при добавлении l к графу 3) l имеет минимальный вес среди ребер, удовлетворяющих условиям 1) и 2).
Теорема. Пусть G = (V, E) и V = n. Тогда граф
Алгоритм Краскал Шаг 1.Тот же, что и в алгоритме Прим. Шаг k. Если граф 1) при добавлении l к графу 2) l имеет минимальный вес среди ребер, удовлетворяющих условию 1). Пример. Дан граф с заданными весами ребер (рис. 1.1). Найти остовное дерево минимального веса.
Рис. 1.1 Решение Приведем два решения с помощью алгоритмов Прим и Краскал. 1) С помощью алгоритма Прим получаем, например, такое остовное дерево минимального веса (рис. 1.2). Последовательность выбираемых ребер: (a, b), (a, f), (a, e), (e, q), (q, h), (h, d), (h, c). Вес дерева: 1+2+2+1+2+1+4=13.
Рис. 1.2
2) С помощью алгоритма Краскал получаем, такое остовное дерево минимального веса (рис.1.3).
Рис. 1.3
Последовательность выбираемых ребер: (a, b), (d, h), (e, q), (q, h), (a, f), (a, e), (b, c). Вес дерева: 1+2+1+1+2+2+3+3=14.
Нахождение кратчайших путей между двумя заданными вершинами. Алгоритм Дийкстры
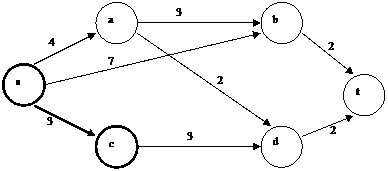
Постановка задачи. Пусть задан ориентированный граф G = (V, E) с заданными положительными длинами ребер l(e)>0, Для решения данной задачи может быть использован алгоритм Дийкстры (Dijkstra E.W., 1959). Идея алгоритма состоит в том, что необходимо упорядочить вершины графа по их расстоянию от s. Предположим, что известны m близлежащих к вершине s вершин и известны сами пути, соединяющие эти вершины с s. Как может быть найдена (m + 1)-я близлежащая к s вершина? Окрасим (пометим) s и m близлежащих к ней вершин. Для каждой неокрашенной вершины u, соседней с одной из окрашенных, построим ребра, соединяющие ее с окрашенными вершинами. После этого выберем кратчайший из путей, соединяющий s с каждой из рассмотренных вершин u. Соответствующая этому кратчайшему пути вершина u является (m + 1)-й близлежащей вершиной. Таким образом, начиная с вершины s (m = 0) и продолжая процедуру окраски до t, можно построить кратчайший путь от s до t. Алгоритм Дийкстры Шаг 1. Вначале алгоритма все вершины не окрашены. Каждой вершине ν во время выполнения алгоритма ставится в соответствие либо число l(ν) — длина кратчайшего пути из s в ν, включающего только окрашенные вершины, либо l’(ν) - временная метка, которая становится равной l(ν) в момент, когда вершина ν окрашивается. Полагаем: l(s) = 0 l’(ν) = ∞, ν ≠ s и окрашиваем вершину s. Шаг 2. Для каждой неокрашенной вершины u, соседней с последней из окрашенных вершин ν, пересчитываем l(u) по формуле: l(u) = min {l’(u), l(ν) + l(ν,u)}, где l(ν, u) - длина дуги между вершинами ν и u. Если l’(u) = ∞ для любой неокрашенной вершины u, то алгоритм следует закончить, так как в исходной сети не существует пути из s в неокрашенные вершины, в том числе и в t. В противном случае находим вершину r, для которой, l’(r) = = min l’(u), после чего вершину r окрашиваем, l(r) = l’(r) и вносим в корневое дерево дугу (ν, r), на которой достигается min в l(r). Вершина r становится последней из окрашенных вершин. Шаг 3. В момент, когда вершина t становится окрашенной, находим кратчайший путь, соединяющий s и t, состоящий из окрашенных дуг (ребер). Теорема. Алгоритм Дийкстры строит в графе G = (V, E) кратчайший (s, t) путь. Пример.Задан граф с фиксированными длинами ребер (рис. 1.4). Найти кратчайший (s, t) путь.
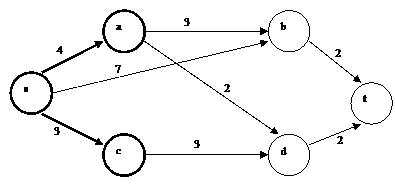
Рис. 1.4 Решение Шаг 1. l(s) = 0, l’(ν) = ∞, ν ≠ s. Окрашиваем вершину s. Шаг 2. Производим перерасчет чисел l(u) для неокрашенных вершин u соседних с s. l’(a) = min {l’(a), l(s) + l(s, a)} = min {∞,0 + 4} = 4, l’(b) = min {l’(b), l(s) + l(s, b)} = min {∞,0 + 7} = 7, l’(c) = min {l’(c), l(s) + l(s, c)} = min {∞,0+ 3} = 3. Таким образом, первой ближайшей к s является вершина c, которую необходимо окрасить (вместе с дугой (s, c)). Получаем l(c) = 3 (рис. 1.5). Так как вершина t является неокрашенной, то необходимо снова повторить шаг 2.
Рис. 1.5
Производим перерасчет меток у вершин, соседних с последней окрашенной вершиной (вершиной с). В данном случае — это единственная вершина d. l’(d) = min {l’(d), l(c) + l(c, d)} = min {∞,3+3} = 6. Метки остальных вершин оставляем без изменения: l’(a) = 4; l’(b) = 7; l’(t) = ∞. Минимум достигается в вершине a. Окрашиваем вершину a и дугу (s, a), на которой достигается минимум. Вершина a становится последней окрашенной вершиной, l(a) = 4 (рис. 1.6). Рис. 1.6 Вершина t по-прежнему не окрашена. Снова повторим шаг 2. Пересчитываем l(u) у вершин, соседних с a — это вершины b и d. l’(b) = min {l’(b), l(a) + l(a, b)} = min {7,4+3} = 7, l’(d) = min {l’(d), l(a) + l(a, d)} = min {6,4+2} = 6, l’(t) = ∞. Окрашиваем вершину d. Величину l(d) определяют как дуга (с, d), так и дуга (a, d). Поэтому можно окрасить любую из этих дуг. Например, пусть это будет (c, d), l(d) = 6. Вершина d становится последней из окрашенных вершин (рис. 1.7).
Рис. 1.7
Так как вершина t не окрашена, то переходим снова к шагу 2. Производим перерасчет меток (это нужно сделать только для вершины t). l’(t) = min {l’(t), l(d) + l(d, t)} = min {∞,6+2} = 8, l’(b) = 7. (рис 1.8).
Рис. 1.8
Вершина b становится последней из окрашенных. Т.к. t не окрашена, то повторяем шаг 2. Производим перерасчет меток (это необходимо сделать только для вершины t, потому что она соседствует с вершиной b). l’(t) = min {l’(t), l(b) + l(b, t)} = min {8,7+2} = 8. Окрашиваем вершину t и дугу (d, t) (рис. 1.9).
Рис. 1.9
Таким образом, построено дерево кратчайших путей из вершины s, включающее и кратчайший (s, t) - путь (s, t) = {(s, c), (c, d), (d, t)}, длина которого равна 8.
Замечание 1. Данное решение в общем случае не является единственным. Кратчайший путь является единственным только в том случае, если в алгоритме ни разу не возникает однозначности в выборе дуг. В данном примере такая неоднозначность возникла и есть соответствующее альтернативное решение: (s, t) = {(s, a), (a, d), (d, t)}. Замечание 2. По алгоритму Дийкстры можно находить кратчайшие пути из вершины s во все другие вершины графа. Для этого следует модифицировать в алгоритме только последний шаг. Если все вершины оказываются окрашенными, то следует закончить алгоритм, иначе перейти к шагу 2. Замечание 3. Данный алгоритм предполагает неотрицательность длин дуг в заданном графе, и поэтому он не применим к графам, в которых есть отрицательные длины (веса) дуг. Для того чтобы в этом убедиться, достаточно рассмотреть следующий граф (рис. 1.10).
Рис. 1.10
Решая его по алгоритму Дийкстры, получаем, что кратчайший (s, t)-путь есть (s, t) = {(s, t)} и его длина равна 1. В действительности, очевидно, что таким путем является путь {(s, a), (a, t)} с нулевой длиной.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 438. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 - неориентированный связный граф. Любой связный подграф
- неориентированный связный граф. Любой связный подграф  , содержащий все вершины графа
, содержащий все вершины графа  выбирается граф, вершинами которого являются вершины графа
выбирается граф, вершинами которого являются вершины графа  уже построен, то граф
уже построен, то граф  получается из
получается из  добавлением ребра l, обладающего следующими свойствами:
добавлением ребра l, обладающего следующими свойствами: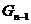 - остовное дерево минимального веса для графа G.
- остовное дерево минимального веса для графа G.

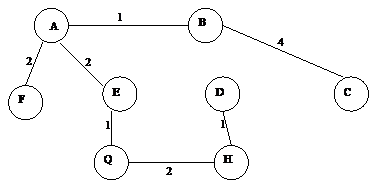
 . Нужно найти длину кратчайшего пути (и сам путь), соединяющего две произвольные фиксированные вершины s и t, где s - начало, а t - конец пути.
. Нужно найти длину кратчайшего пути (и сам путь), соединяющего две произвольные фиксированные вершины s и t, где s - начало, а t - конец пути.