
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Собственные векторы и собственные значения⇐ ПредыдущаяСтр 12 из 12
Вектор
Число
Вектор
или
Система (65) имеет нулевое решение. Для того, чтобы она имела ненулевое решение необходимо и достаточно, чтобы
Определитель матрицы Пусть оператор
( Следовательно, матрица оператора
Верно и обратное: если Например, найти собственные значения и собственные векторы линейного оператора

Решение. Составим характеристическое уравнение:
Находим собственные векторы:
1) при
Получим систему однородных уравнений:
2) при
Получим систему однородных уравнений:
3) при
Получим систему однородных уравнений:
Вектора Нормируем полученные собственные векторы. Подберем
Ответ:
Линейная модель обмена (модель международной торговли)
Пусть имеется n стран Пусть
Составим матрицу Выручка от торговли для любой страны
Для баланса торговли необходимо, чтобы выручка от торговли для каждой страны была не меньше, чем ее национальный доход. Такое условие называется условием бездифицитности:
Рассмотрим матричное уравнение
Таким образом, задача свелась к отысканию собственного вектора матрицы Например, требуется найти соотношение цен трех товаров, если набор этих товаров Пусть имеется три вида товаров
Например, при Ответ: 15:10:3 – соотношение цен трех товаров.
Квадратичные формы
Квадратичной формой
где
Матрица Например, для квадратичной формы трех переменных Решение. Составим матрицу, используя свойство (74):
Ранг матрицы Пусть задана матрица переменных
Пусть заданы две матрицы
соотношением:
Вывод: при невырожденном линейном преобразовании
Квадратичная форма (73) называется канонической, если все ее коэффициенты
Ранг квадратичной формы равен числу не равных нулю коэффициентов канонической формы. Теорема: Любая квадратичная форма (73) с помощью невырожденных линейных преобразованиях переменных может быть переведена в канонический вид (77). Такое преобразование не единственное, одна и та же квадратичная форма может быть приведена к каноническому виду по-разному. Но при этом различные канонические формы обладают рядом общих свойств: ранг матрицы квадратичной формы не меняется при линейных преобразованиях. Среди приемов перевода квадратичной формы в каноническую форму можно выделить две: 1) выделение полных квадратов для переменных; 2) использование ортогональных преобразований. Пусть задана квадратичная форма
Квадратичная форма переходит в каноническую форму:
Квадратичная форма (73) называется положительно (отрицательно) определенной, если при всех переменных, из которых хотя бы одно отлично от нуля, выполняется условие: Теорема 1: для того, чтобы форма Теорема 2 (критерий Сильвестра): для того, чтобы квадратичная форма Если квадратичная форма не поддается определению, то ее называют знаконеопределенной.
Упражнения
1. В пространстве 2. Найти собственные числа и собственные векторы матрицы:
а) 3. В базисе 4. Привести к каноническому виду квадратичную форму: а) б) Составить матрицы квадратичной формы. 5. Исследовать на знакоопределенность квадратичные формы: а) б) Составить матрицы квадратичной формы. 6. Найти соотношение цен трех товаров, если наборы этих товаров
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 180. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 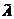 , если найдется такое число
, если найдется такое число  , что
, что (62)
(62)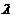 , соот-ветствующим вектору
, соот-ветствующим вектору  :
: (63)
(63) (64)
(64) (65)
(65) (66)
(66)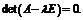 (67)
(67) называется характеристическим многочленом оператора
называется характеристическим многочленом оператора  или матрицы
или матрицы  , а само уравнение (67) называется характеристическим уравнением
, а само уравнение (67) называется характеристическим уравнением 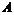 .
. (матрица
(матрица  ) имеет
) имеет 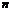 линейно независимых собственных векторов
линейно независимых собственных векторов  с собственными числами
с собственными числами  . Векторы
. Векторы  примем за базисные. Тогда
примем за базисные. Тогда ,
, , если
, если  и
и  , если
, если  ).
). (68)
(68)
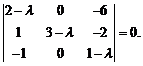
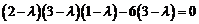 ,
, 
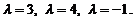

 ;
;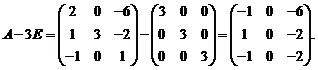



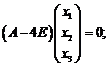





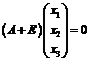 ;
;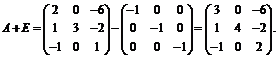


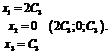
 при
при 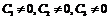 являются собственными векторами. Числа
являются собственными векторами. Числа 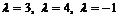 - собственные значения.
- собственные значения. так, чтобы длина вектора равнялась единице:
так, чтобы длина вектора равнялась единице: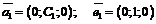 .
.
 .
.


 . Национальный доход каждой страны
. Национальный доход каждой страны  .
. - доля национального дохода, которую страна
- доля национального дохода, которую страна  тратит на покупку товаров страны
тратит на покупку товаров страны  . Предположим, что национальный доход тратится либо на закупку товаров или внутри страны, на импорт из других стран, следовательно, выполняется условие:
. Предположим, что национальный доход тратится либо на закупку товаров или внутри страны, на импорт из других стран, следовательно, выполняется условие: (69)
(69)  , которая называется структурной матрицей торговли. Сумма в столбцах равна единице.
, которая называется структурной матрицей торговли. Сумма в столбцах равна единице. равна:
равна: . (70)
. (70)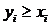 (71)
(71) . Его можно записать так:
. Его можно записать так: . (72)
. (72)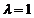 .
. имеют одинаковую стоимость.
имеют одинаковую стоимость. и их цены
и их цены  . Составим систему уравнений:
. Составим систему уравнений:


 , следовательно
, следовательно 

 .
. ,
,  .
. от
от  переменных называется сумма
переменных называется сумма (73)
(73) -действительные числа, причем
-действительные числа, причем . (74)
. (74)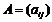 ,
, 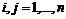 ,называется матрицей квадратичной формы. Матрица
,называется матрицей квадратичной формы. Матрица  составить матрицу.
составить матрицу.
 . Выражение (73) в матричной форме запишется так:
. Выражение (73) в матричной форме запишется так: (75)
(75)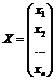 и
и  , которые связаны
, которые связаны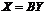 , где матрица
, где матрица  ,
,  , является невырожденной матрицей перехода от матрицы
, является невырожденной матрицей перехода от матрицы 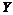 к матрице
к матрице  Тогда
Тогда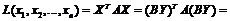
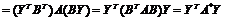
 матрица квадратичной формы (73) принимает вид:
матрица квадратичной формы (73) принимает вид: (76)
(76)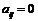 при
при  , а матрица
, а матрица  (77)
(77) , известна ее матрица
, известна ее матрица  . Найдем собственные значения и собственные векторы этой матрицы. Пусть имеется матрица перехода
. Найдем собственные значения и собственные векторы этой матрицы. Пусть имеется матрица перехода  от одного ортонормированного базиса
от одного ортонормированного базиса  в другой
в другой  :
: , (78)
, (78) - нормированные собственные векторы, соответствующие собственным числам
- нормированные собственные векторы, соответствующие собственным числам  . Имеем формулы перехода:
. Имеем формулы перехода: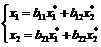 . (79)
. (79) ,
, 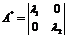 . (80)
. (80) Существуют разные методы определения знака квадратичной формы.
Существуют разные методы определения знака квадратичной формы. была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения
была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения  матрицы
матрицы  была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны:
была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны:  ;дляотрицательно определенной квадратичной формы знаки главных миноров должны чередоваться, начиная с отрицательного значения:
;дляотрицательно определенной квадратичной формы знаки главных миноров должны чередоваться, начиная с отрицательного значения: 

 линейный оператор
линейный оператор  в базисе
в базисе  задан матрицей
задан матрицей  . Найти образ
. Найти образ  вектора
вектора  .
. ; б)
; б)  ; в)
; в) 
 . Найти матрицу оператора
. Найти матрицу оператора  ;
;  .
.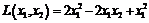 ;
;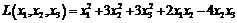
 ;
;
