
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проекции вектора в прямоугольной системе координат Пусть в пространстве задана система координат XYZO и произвольный вектор Проекции X, Y, Z вектора Теорема 6. Каковы бы ни были точки
Следствие 1: если
Следствие 2:
Следствие 3: Если
Следствие 4: Если Следствие 5: Если
Направляющиеся косинусы вектора Пусть дан произвольный вектор
В силу определения проекции вектора на ось получим:
Выразим косинусы углов, которые называются направляющими косинусами:
Основное свойство косинусов:
Разложение вектора по базису
Упорядоченная тройка неколлинеарных векторов
где Теорема.Любой вектор 
Такое представление называется разложением по базису Например, записать разложение вектора
Скалярное произведение векторов Скалярным произведением двух ненулевых векторов
или
Типичным примером скалярного произведения в физике является формула работы Свойства скалярного произведения векторов: 1. 2. 3. 4. 5. Скалярное произведение можно находить в координатах. Справедлива теорема: если векторы
Следствие 1:
Следствие 2: |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 167. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
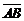 .
. на оси координат называются его координатами, при этом пишут:
на оси координат называются его координатами, при этом пишут:  .
. ,
, 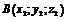 координаты вектора
координаты вектора  определяются по формулам:
определяются по формулам: (29)
(29) , то координаты
, то координаты  равны координатам его конца;
равны координатам его конца; (30)
(30) и
и 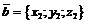 , то
, то  (31)
(31) (32)
(32)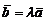 , то
, то  (33)
(33) , выходящий из начала координат, не совпадающий с осями координат образующий с ними углы
, выходящий из начала координат, не совпадающий с осями координат образующий с ними углы  . Найдем длину вектора:
. Найдем длину вектора: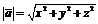 .
. ,
,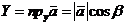 , (34)
, (34) .
. ,
,  , (35)
, (35) .
.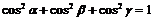 .
. называется базисом и любой вектор
называется базисом и любой вектор  может быть единственным образом представлен в виде линейной комбинации векторов
может быть единственным образом представлен в виде линейной комбинации векторов  :
: , (36)
, (36) - координаты вектора
- координаты вектора  в базисе векторов (
в базисе векторов (  ). В прямоугольной системе координат за базис выбирают единичные вектора осей координат:
). В прямоугольной системе координат за базис выбирают единичные вектора осей координат: 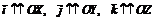 ,
, 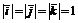 . Тогда справедлива теорема.
. Тогда справедлива теорема. может быть единственным образом представлен в виде
может быть единственным образом представлен в виде - числа. (37)
- числа. (37) ,а вектор
,а вектор  .
. по базису
по базису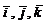 . Вектор будет иметь вид:
. Вектор будет иметь вид: 
 называется число (скаляр) равное произведению длин этих векторов на косинус угла между ними:
называется число (скаляр) равное произведению длин этих векторов на косинус угла между ними: , (38)
, (38)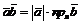 =
= 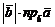 (39)
(39) , где
, где  - сила, точка приложения которой перемещается на расстояние
- сила, точка приложения которой перемещается на расстояние 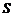 .
. ;
; ;
; ;
;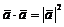 ;
; , если
, если  , и, обратно,
, и, обратно,  , если
, если  .
. ,
,  , то их скалярное произведение определяется формулой:
, то их скалярное произведение определяется формулой: (40)
(40) , если
, если  (41)
(41) (42)
(42)