
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение линейного оператора Пусть заданы два линейных пространства: Вектор Оператор Оператор Оператор 1) 2) Пусть в пространстве
………………………
Распишем
+
=
+
С другой стороны
…………………….
Матрица коэффициентов данной системы называется матрицей оператора Вывод:каждому линейному оператору Введем для векторов Тогда систему равенств можно записать в виде матричного уравнения:
Рассмотрим пример. Найти образ 
Решение. Найдем матрицу
Следовательно, образ вектора Действия над операторами 1. Суммой операторов 2. Произведением оператора 3. Произведением операторов Сами операторы
Матрица оператора в новом базисе Пусть задано два базиса Из условия
Следовательно,
Например, найти матрицу Составим матрицу перехода из базиса в базис: Найдем обратную матрицу для матрицы Тогда
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Если задан закон, по которому каждому вектору
. Если задан закон, по которому каждому вектору  ставится в соответствие единственный вектор
ставится в соответствие единственный вектор 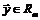 , то говорят, что задан оператор (преобразование, отображение)
, то говорят, что задан оператор (преобразование, отображение)  , действующий из
, действующий из  в
в  , и пишут
, и пишут . (59)
. (59) , вектор
, вектор 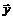 . Если пространства совпадают, то оператор
. Если пространства совпадают, то оператор  называется нулевым,если переводит все векторы
называется нулевым,если переводит все векторы  .
. называется тождественным, если переводит любой вектор
называется тождественным, если переводит любой вектор  .
. и любого действительного числа
и любого действительного числа  выполняются равенства:
выполняются равенства: (свойство аддитивности);
(свойство аддитивности);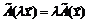 (свойство однородности).
(свойство однородности). . Любой вектор
. Любой вектор  . Тогда
. Тогда  . Каждый из векторов
. Каждый из векторов  можно разложить по базису
можно разложить по базису 


 +
+  +…
+… =
= +
+  +…
+… .
. . Так как разложение по базису единственное, то справедливы равенства:
. Так как разложение по базису единственное, то справедливы равенства:

 .
. -го порядка соответствует линейный оператор
-го порядка соответствует линейный оператор  ,
,  .
. . (60)
. (60)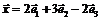 , если оператор
, если оператор  .
. .
.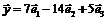 .
. называется оператор
называется оператор  , такой, что
, такой, что  .
.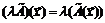 .
.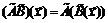 .
.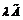 ,
,  являются линейными.
являются линейными. в пространстве
в пространстве  оператора
оператора 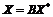 и
и  , где
, где  - матрица перехода из базиса векторов
- матрица перехода из базиса векторов  .
.  ,
,  ,
,  ,
,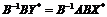 ,
,  ,
, . (61)
. (61) линейного оператора в базисе
линейного оператора в базисе 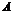 в базисе
в базисе  ,
,  ,
,  .
.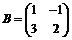 .
. .
.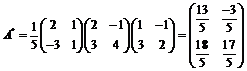 .
.