Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы решения систем линейных уравнений1)Метод Крамера. Теорема Крамера: Пусть D - главный определитель системы, состоящий из коэффициентов при неизвестных; Dj – определители, полученные из главного, заменой j –того столбца этого определителя столбцом свободных членов. Тогда, если D¹0, то система имеет единственное решение, определяемое равенствами:
Формула (14) называется формулой Крамера. Исследование наличия решения системы: а) если б) если в) если Например, найти решение системы уравнений
Решение: найдем главный определитель системы
Составим определители для неизвестных и вычислим их:
Ответ:
2)Метод обратных матриц. Систему линейных уравнений (12) представим в матричной форме:
Найдем решение уравнения: Решение системы можно записать так:
Например, найти решение системы уравнений матричным методом
Решение: введем матрицы:
Определитель матрицы Найдем обратную матрицу:
Вычислим матрицу
Ответ:
3)Метод Гаусса. Метод Гаусса иначе называется методом исключения переменных. Метод основан на преобразовании уравнений с использованием преобразований, называемых гауссовыми.  К преобразования Гаусса относятся следующие действия: а) можно менять уравнения системы местами; б) умножать уравнение на любое число, не равное нулю; в) к любому уравнению, умноженному на число, не равное нулю, можно прибавлять другое уравнение, умноженное на любое число, не равное нулю. Суть метода Гаусса: 1) в системе выбираем уравнение, в котором имеется неизвестное с ненулевым коэффициентом (лучше выбирать коэффициент 1). Это уравнение объявляем ведущим, а неизвестное, подлежащее исключению, называем главным. 2) ведущее уравнение ставим на первое место и с помощью преобразований Гаусса исключаем главное неизвестное из остальных уравнений; 3) данную процедуру применяем к следующим уравнениям. Например, найти решение системы уравнений методом Гаусса
Решение: запишем систему в виде расширенной матрицы коэффициентов при неизвестных и свободных членов; используя преобразования Гаусса, приведем матрицу к треугольному виду:
Теперь вычислим неизвестные:
Ответ:
В результате исключения неизвестных последнее уравнение может иметь вид: 1) 2) 3) Например, найти все базисные решения системы уравнений
Решение: система имеет три уравнения и четыре неизвестных. Выполним преобразования матрицы коэффициентов:
Ранг матрицы коэффициентов
одну строку можно отбросить. Получим систему
Найдем число базисных решений:
1) Пусть базисными будут
Тогда первое базисное решение будет иметь вид 2) Пусть базисными будут
Тогда первое базисное решение будет иметь вид
3) Пусть базисными будут
Тогда первое базисное решение будет иметь вид 4) Пусть базисными будут
Тогда первое базисное решение будет иметь вид 5) Пусть базисными будут
Тогда первое базисное решение будет иметь вид 6) Пусть базисными будут
Тогда первое базисное решение будет иметь вид
Ответ: получили шесть базисных решений:
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 168. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (14)
(14) система имеет единственное решение;
система имеет единственное решение; но хотя бы один из определителей для неизвестных не равен нулю, то система не имеет решения;
но хотя бы один из определителей для неизвестных не равен нулю, то система не имеет решения; и все определители для неизвестных равны нулю, то система имеет множество решений.
и все определители для неизвестных равны нулю, то система имеет множество решений.
 .
.





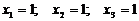 .
. .
. 
 (15)
(15)
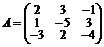 ;
; 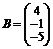 .
. уже найден
уже найден  Следовательно, обратная матрица существует.
Следовательно, обратная матрица существует. .
. :
:
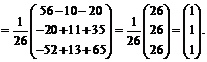
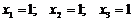 .
.
 =
=  =
= 
 ,
,  ,
,  .
.
 , то система имеет единственное решение;
, то система имеет единственное решение;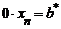 , то система не имеет решения;
, то система не имеет решения; , то система имеет множество решений.
, то система имеет множество решений.
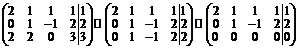 .
. . Следовательно,
. Следовательно,
 .
. и
и 
 ,
, 

 .
. .
.
 ,
, 
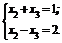
 .
. .
.


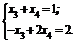

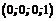 .
. ,
, 


 .
. ,
, 


 .
.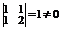 ,
, 


 .
.