
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейная зависимость векторов Вектор
Векторы
Если равенство (49) выполняется только при Теорема: если векторы На плоскости два линейно независимых вектора – это не коллинеарные вектора. Тогда любой третий вектор можно представить в виде: В пространстве три некомпланарных вектора можно считать линейно независимыми и любой четвертый представить в виде:
Свойства векторов линейного пространства: 1) если среди векторов 2) если часть векторов Например, проверим, являются ли векторы линейно зависимыми
Решение. Составим равенство:
Пусть
Размеренность и базис векторного пространства Векторное (линейное) пространство пространство, Множество n независимых векторов n-мерного пространства  Пусть имеется n-мерное пространство
где Выражения (50), (51) являются разложениями вектора Теорема: если Покажем, что следующие вектора образуют базис
Решение: если
Переход к новому базису Пусть пространство
Матрица коэффициентов этой системы называется матрицейперехода от старого
Обратный переход от Пусть задан вектор 1) в базисе 2) в базисе Тогда
Например, в базисе Решение: а) Покажем, что
следовательно векторы образуют базис. б) Выразим связь между базисами:
в) Найдем обратную матрицу А-1
г) По формуле (47) найдем координаты
Скалярное произведение векторов. Евклидово пространство Пусть заданы два вектора в пространстве
Свойства скалярного произведения: 1. 2. 3. 4. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющих свойствам 1-4, называется евклидовым пространством. Длиной (нормой, модулем) вектора
Свойства длины вектора: 1) 2) 3) 4) Угол между векторами определяется по формуле:
Два вектора называются ортогональными, если их скалярное произведение равно нулю:
Вектор Если единичные векторы Теорема: Во всяком n-мерном евклидовом пространстве существует ортонормированный базис. Например, в трехмерном пространстве таким базисом является система векторов
Упражнения 1.Определить, являются ли векторы 2. В базисе 3. В базисе 4. В базисе 5. Найти длину вектора 6. Найти косинус угла между векторами 7. При каком значении параметра
7. Линейные операторы
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 192. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется линейной комбинацией векторов
называется линейной комбинацией векторов  векторного пространства
векторного пространства  , если выполняется равенство
, если выполняется равенство (48)
(48) -любые числа.
-любые числа. называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа  (49)
(49) , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми. .
. .
. , то эти векторы линейно зависимы;
, то эти векторы линейно зависимы; ?
? ,
,
 .
. ,
, 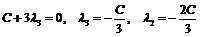 . Система имеет множество решений
. Система имеет множество решений  . Следовательно, заданные векторы линейно зависимые.
. Следовательно, заданные векторы линейно зависимые. линейно независимых векторов, а любые
линейно независимых векторов, а любые  векторов – линейно зависимые.
векторов – линейно зависимые.  . Например,
. Например,  ,
, 
 ,
,  – базис
– базис  Любой вектор
Любой вектор  - линейно зависимый, следовательно,
- линейно зависимый, следовательно, ,
, ,
, 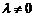 (50)
(50) , (51)
, (51) - координаты вектора
- координаты вектора  по базису
по базису  – координаты вектора
– координаты вектора  линейно выражается через них, то пространство
линейно выражается через них, то пространство  .
. образуют базис, то они линейно независимы, следовательно
образуют базис, то они линейно независимы, следовательно  :
: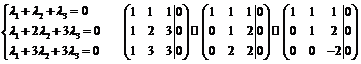
 - линейно-независимые векторы и составляют базис.
- линейно-независимые векторы и составляют базис.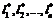 - новый:
- новый: (52)
(52)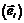 к новому
к новому  базису:
базису: (53)
(53) (в старом),
(в старом), (в новом).
(в новом). или
или 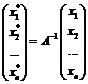 (54)
(54) заданы векторы
заданы векторы 

 и
и  . Выразить вектор
. Выразить вектор  в базисе векторов
в базисе векторов  .
. ,
, матрица перехода
матрица перехода  .
. .
. .
. и
и  . Скалярным произведением двух векторов
. Скалярным произведением двух векторов  называется число, вычисляемое по формуле:
называется число, вычисляемое по формуле: . (55)
. (55) ,
, ,
, , где
, где 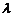 - действительное число,
- действительное число, , если
, если  ,
,  , если
, если 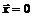 ,
, 
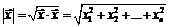 . (56)
. (56) ;
; - действительное число;
- действительное число; - неравенство Коши-Буняковского;
- неравенство Коши-Буняковского; - неравенство треугольника.
- неравенство треугольника. ,
, 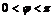 . (57)
. (57) . (58)
. (58)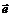 называется единичным,если
называется единичным,если  .
. n-мерного евклидового пространства попарно ортогональны и норма каждого вектора равна 1, то векторы
n-мерного евклидового пространства попарно ортогональны и норма каждого вектора равна 1, то векторы  .
. ,
,  ,
,  линейно зависимыми.
линейно зависимыми. заданы векторы
заданы векторы  ,
, 
 . Показать, что они образуют базис и в этом базисе выразить вектор
. Показать, что они образуют базис и в этом базисе выразить вектор  .
.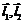 заданы векторы
заданы векторы  ,
,  . Показать, что они образуют базис и в этом базисе выразите вектор
. Показать, что они образуют базис и в этом базисе выразите вектор 

 . Найти вектор
. Найти вектор  в этом базисе.
в этом базисе.
 и
и  векторы
векторы  и
и  ортогональны.
ортогональны.