
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нахождение обратной матрицы методом элементарных преобразований
Элементарные преобразования матриц можно использовать для получения обратных матриц, присоединяя к данной матрице единичную матрицу: Например, для матрицы
Используем метод элементарных преобразований, получим:
~
~
~ Протокол действий: 1) элементы второй строки умножим на (-1) и поменяем местами с первой строкой; 2) от второй строки отнимем две первых строки (С2-2С1); 3) поделим вторую строку на 9 и третью строку на 2; 4) от третьей строки отнимем вторую строку (С3-С2); 5) поделим третью строку на 4/3; 6) из второй строки вычтем третью, умноженную на 2/3 (С2-2/3С3); 7) к первой строке прибавим три вторых строки и одну третью (С1+3С2+С3). В результате получили обратную матрицу
Упражнения
1) А+3В-2С, если
2) АВ+ВС, если
3) АВ-Е и ВА-Е, если
4) Е-(А-В)С, если
А-1А=АА-1=Е, если
1)
4. Найти ранг матрицы:
1)
4) Решение систем линейных уравнений
Общие сведения Системой m линейных уравнений с n неизвестными называется система вида
где Если система (12) имеет решение, то она называется совместной. Если система не имеет решения, то она называется несовместной. Если система (12) имеет единственной решение, то она называется определенной. Если система имеет множество решений, она называется неопределенной.  Если все свободные члены системы (12) равны нулю, система называется однородной. Такая система всегда совместна, имеет тривиальное решение – нулевое. Введем в рассмотрение следующие матрицы: 1) матрица коэффициентов при неизвестных
А= 2) матрица неизвестных 3) матрица свободных членов
Тогда система уравнений может быть записана в матричном виде:
Вопрос о совместности системы помогает решить теорема Кронекера-Капелли. Теорема: Для того, чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы Матрица Если ранг матрицы А равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы А меньше числа неизвестных, то система имеет множество решений. При условии Пусть
Остальные 1) С=0 для базисных решений; 2) С=Сi для общего решения; 3) С равно строкам единичной матрицы для фундаментального решения.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 207. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. найти обратную матрицу.
найти обратную матрицу. ~
~  ~
~  ~
~ ~
~  ~
~ ~
~  ~
~
 .
.


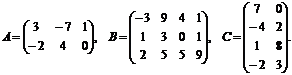
 .
. 2)
2)  3)
3) 
 2)
2)  3)
3) 

 (12)
(12) - коэффициенты при неизвестных,
- коэффициенты при неизвестных,  - свободные члены,
- свободные члены,  – неизвестные.
– неизвестные. ,
, ,
, .
.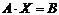 . (13)
. (13) .
.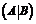 называется расширенной матрицей системы.
называется расширенной матрицей системы. уравнения системы зависимые. При условии
уравнения системы зависимые. При условии  уравнения системы независимые.
уравнения системы независимые.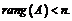 Переменные
Переменные  называются базисными, основными, если базисный минор (определитель из коэффициентов при этих переменных) не равен нулю. Их число равно
называются базисными, основными, если базисный минор (определитель из коэффициентов при этих переменных) не равен нулю. Их число равно  Число базисных решений меньше числа сочетаний
Число базисных решений меньше числа сочетаний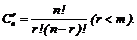
 неизвестных называются не основными (свободными). Свободным переменным в решении могут присваиваться следующие значения:
неизвестных называются не основными (свободными). Свободным переменным в решении могут присваиваться следующие значения: