
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы вычисления ранга матрицыСтр 1 из 12Следующая ⇒ Определители Определитель второго порядка Пусть задана таблица четырех чисел, расположенных в две строки и в два столбца
Элементы а11, а12 – образуют первую строку, элементы а21, а22 образуют вторую строку. Элементы а11, а21 образуют первый столбец, элементы а12, а22 образуют второй столбец. Элементы а11, а22 стоят на главной диагонали, элементы а12, а21 стоят на побочной диагонали. Определителем второго порядка для чисел (1) называется число, которое вычисляется по формуле
а11а22 – а12а21 (2)
Иначе это определение можно дать так: определителем второго порядка для чисел (1) называется число, равное разности произведений элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали. При этом пишут
Определитель (от латинского слова determinant) обозначается
Например, вычислить определитель
Решение: Определитель третьего порядка
Пусть задана таблица, состоящая из девяти чисел, расположенных в три строки и три столбца
Определителем третьего порядка для таблицы чисел (4) называется число, которое вычисляется по формуле
при этом пишут
Для вычисления определителя третьего порядка можно использовать правило, называемое правилом "треугольника":  - три первых слагаемых в формуле (5) берутся со знаком плюс и мысленно строятся треугольники с основаниями параллельными главной диагонали и с вершинами в элементах на побочной диагонали (рис.1);
Рис. 1
(рис.2).
Рис.2
Например, вычислить определитель третьего порядка по правилу
«треугольника» Решение:
Минор определителя Пусть задан определитель третьего порядка Минором любого элемента
Например, для определителя Решение: а) минор М11 получим, вычеркивая первую строку и первый столбец определителя:
М11= б) для получения минора М32 вычеркнем третью строку и второй столбец определителя: М32=
Алгебраическое дополнение Алгебраическим дополнением любого элемента определителя
Например, для определителя Решение:
Разложение определителя по строке или столбцу Теорема: В выражении (7) записано разложение определителя по элементам i строки. Аналогичное разложение можно записать по любой строке или столбцу. Например, записать разложение определителя Решение: 1) Вычислим определитель разложением по второй строке:
2) Вычислим этот же определитель разложением по третьему столбцу:
Свойства определителей
1. Значение определителя не изменится, если строчки и столбцы определителя поменять местами:
2. Значение определителя изменится на противоположное по знаку, если две строки или два столбца определителя поменять местами:
3. Общий множитель элементов строки или столбца определителя можно вынести за знак определителя:
4. Определитель равен нулю, если он имеет строку или столбец, состоящий из нулей. 5. Определитель равен нулю, если он имеет две одинаковых строки или два одинаковых столбца. 6. Определитель равен нулю, если он имеет две пропорциональные строки или два пропорциональных столбца. 7. Значение определителя не изменится, если к элементам одной строки или столбца прибавить элементы другой строки или столбца, умноженные на какое-то число:
Например, вычислить определитель четвертого порядка, используя свойства определителей и разложение определителя по первой строке:
Решение: прежде чем вычислить определитель, получим в первой строчке нули, во втором и четвертом столбцах. Для этого умножим первый столбец на (-2) и сложим со вторым, второй столбец изменится, и умножим первый столбец на (-3) и сложим с четвертым, изменится четвертый столбец:
Решим этот же пример, получив нули в третьем столбце. Для этого к третьей строке прибавим вторую, изменится третья строка, и к четвертой строке прибавим вторую строку, умноженную на (-5), изменится четвертая строка:
Упражнения 1. Вычислить определители второго и третьего порядка:
1) 5)
8)
2. Решить уравнения и неравенства: 1)
4)
3. Разложить определитель по указанной строке или столбцу и вычислить его.
1)
2)
4.Вычислить определители, используя их свойства:
1)
2. Матрицы
Определение Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Размер матрицы – Например, задана матрица
Виды матриц 1) Матрица размером 2) Матрица размером 3) Матрица размером Если определитель такой матрицы равен нулю, то матрица называется вырожденной, в противном случае – невырожденной.
Например, для матрицы
Определитель матрицы равен:
4) Матрица, у которой число строк и столбцов не равны, называется прямоугольной. 5) Матрица, элементами которой являются нули, называется нуль-матрицей О. 6) Матрица, элементы которой задаются по формуле
7) Диагональная матрица размером
задаются по формуле
обозначается Е. 8) Матрицы одного размера 9) Противоположной для матрицы А называется матрица тех же размеров
Операции над матрицами
1) Сложение матриц. Суммой матриц Аm
Свойства: 1. 2. 3. 4. 2) Умножение матриц на число. При умножении матрицы А на число α получается матрица С = α·А, элементы которой определяются по формуле:
Свойства: 1. 2. 3. 4. 5. 6. 3) Умножение матриц. Произведением матрицы
то есть определяется сумма произведений соответствующих элементов i – строки матрицы А на соответствующие элементы j – столбца матрицы В. Матрицы можно умножать, если внутренние размерности совпадают. Свойства: 1. 2. 3. 4. Если выполняется условие Например, выполнить действия с матрицами
Решение. Умножим матрицы на числа:
Найдем сумму матриц
Найдем произведение матриц
Найдем разность матриц
Транспонированная матрица Матрица АТ называется транспонированной к матрице А, если в матрице А строчки и столбцы поменять местами. Свойства транспонированных матриц:
1) 2) 3) 4) Например, для матрицы Решение: транспонированной является матрица:
Обратная матрица Матрица
Необходимые условия существования обратной матрицы: 1) матрица 2) определитель матрицы Алгоритм нахождения обратной матрицы: 1. составить определитель матрицы 2. если 3. если 4. транспонировать присоединенную матрицу 5. записать обратную матрицу: Например, найти обратную матрицу для матрицы А: Найдем определитель матрицы А:
Найдем алгебраические дополнения для элементов матрицы А:
Составим присоединенную матрицу:
Транспонируем матрицу
Обратная матрица имеет вид:
Для проверки правильности вычислений следует выполнить умножение:
Ранг матрицы Минором матрицы
Например, для матрицы
Рангом матрицы Свойства ранга матрицы: 1) 2) 3) если
Методы вычисления ранга матрицы
1. Метод окаймляющих миноров. Пусть задана матрица а) выбирается любой элемент матрицы, неравный нулю, и около него строится определитель второго порядка; б) если построенный определитель не равен нулю, то около него строится определитель третьего порядка; в) если все определители третьего порядка равны нулю, и миноры большего порядка построить нельзя, то 2. Метод элементарных преобразований матриц. Теорема: ранг матрицы не изменится при элементарных преобразованиях матрицы. Элементарные преобразования матриц: 1) отбрасывание строки, состоящей из нулей; 2) умножение элементов строки на любое число, не равное нулю; 3) изменение порядка строк; 4) прибавление к элементам одной строки элементов другой строки, умноженных на любое число, не равное нулю; 5) транспонирование матрицы. После элементарных преобразований матрицу приводят к матрице трапецеидального вида. Например, для матрицы Первый метод. Найдем миноры первого, второго и третьего порядков, выстраивая их около первого члена матрицы:
Ответ: Второй метод. Приведем матрицу к трапециидальному виду:
Протокол действий: 1) переставили первый и четвертый столбцы местами; 2) от второй строки отняли четыре первых строки (С2 – 4С1); 3) от третьей строки отняли две первых (С3- 2С1); 4) из второго столбца вычли четвертый столбец. Теперь легко найти неравный нулю минор максимального порядка и ранг матрицы:
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 245. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) (3)
(3) или
или 

 .
. (4)
(4) (5)
(5)
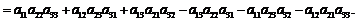 .
.
 - три следующих слагаемых берутся со знаком минус и мысленно строятся треугольники с основаниями параллельными побочной диагонали и с вершинами в элементах, стоящих на главной диагонали
- три следующих слагаемых берутся со знаком минус и мысленно строятся треугольники с основаниями параллельными побочной диагонали и с вершинами в элементах, стоящих на главной диагонали



 , где i – индекс строки, j – индекс столбца.
, где i – индекс строки, j – индекс столбца.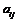 определителя
определителя  , называется определитель меньшего порядка, который получен из элементов определителя, оставшихся после вычеркивания элементов i – строки и j – столбца. Обозначается минор
, называется определитель меньшего порядка, который получен из элементов определителя, оставшихся после вычеркивания элементов i – строки и j – столбца. Обозначается минор 
 найти миноры М11, М32.
найти миноры М11, М32. ;
; .
. называется минор этого элемента с определенным знаком:
называется минор этого элемента с определенным знаком: 
 (6)
(6) ,
,  .
. определитель n-ого порядка равен сумме произведений элементов выбранной строки или столбца на их алгебраические дополнения:
определитель n-ого порядка равен сумме произведений элементов выбранной строки или столбца на их алгебраические дополнения: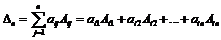 (7)
(7)



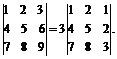
 .
. .
.
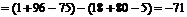 .
.
 .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 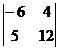 ;
;  ; 6)
; 6)  ; 7)
; 7)  ;
; 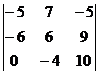 ; 9)
; 9) 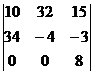 ; 10)
; 10)  .
. ; 2)
; 2)  ; 3)
; 3) 
 ; 5)
; 5)  ;6)
;6)  .
. по первой строке и четвертому столбцу;
по первой строке и четвертому столбцу; по третьей строке и первому столбцу.
по третьей строке и первому столбцу. ; 2)
; 2)  .
. . Обозначаются матрицы большими латинскими буквами
. Обозначаются матрицы большими латинскими буквами  . Элементы матриц обозначаются маленькими буквами:
. Элементы матриц обозначаются маленькими буквами:  , где i – номер строки, j – номер столбца.
, где i – номер строки, j – номер столбца. :
: .
. называется матрицей-строкой.
называется матрицей-строкой. называется матрицей-столбцом.
называется матрицей-столбцом. называется квадратной порядка m. Для такой матрицы можно составить определитель, состоящий из элементов матрицы.
называется квадратной порядка m. Для такой матрицы можно составить определитель, состоящий из элементов матрицы. найти определитель.
найти определитель. .
. , называется диагональной.
, называется диагональной.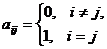 , называется единичной и
, называется единичной и и
и  называются равными, если их соответствующие элементы равны (
называются равными, если их соответствующие элементы равны (  ).
). , определенная следующим образом:
, определенная следующим образом:  .
. n и Bm
n и Bm  . (8)
. (8) ;
; ;
; ;
;  - нулевая матрица;
- нулевая матрица; .
. . (9)
. (9) ;
;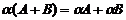 ;
; ;
; ;
; ;
;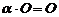 .
. называется матрица
называется матрица 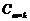 , элементы которой определяются по формуле:
, элементы которой определяются по формуле: (10)
(10) ;
; ;
; ;
; .
. , то матрицы
, то матрицы  называются перестановочными.
называются перестановочными. ;
;  , если
, если  ;
;  .
. ,
,  .
. .
.  :
:
 .
. .
.



 построить транспонированную матрицу.
построить транспонированную матрицу. .
. называется обратной матрицей для матрицы
называется обратной матрицей для матрицы  . (11)
. (11)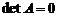 , то обратная матрица не существует;
, то обратная матрица не существует; , составить присоединенную матрицу
, составить присоединенную матрицу  , состоящую из алгебраических дополнений к элементам матрицы А;
, состоящую из алгебраических дополнений к элементам матрицы А; ;
;
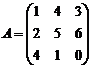 .
.
 ;
;  ;
; 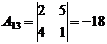 ;
; ;
;  ;
;  ;
; ;
;  ;
;  .
.
 :
: .
. .
.
 найти все миноры второго порядка.
найти все миноры второго порядка. ,
,  ,
,  .
. или
или  . В примере миноры второго порядка не равны нулю, то
. В примере миноры второго порядка не равны нулю, то  .
. ;
;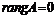 , если все элементы матрицы А равны нулю;
, если все элементы матрицы А равны нулю; , то
, то 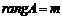 .
. :
: , если найдется хотя бы один определитель третьего порядка не равный нулю, то
, если найдется хотя бы один определитель третьего порядка не равный нулю, то 
 найти ранг матрицы обоим методами.
найти ранг матрицы обоим методами.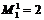 ,
,  ,
,  .
. .
. ~
~ 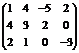 ~
~  ~
~  .
.