
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Мат.ожидание непрерывной С.В.Пусть непрерывная С.В X задана плотностью распределения f(x). Допустим, что все возможные значения X принадлежат отрезку [a; b]. Разобьем этот отрезок на n частичных отрезков длиной Перейдем к пределу: Свойства математического ожидания: 1. Мат. ожидание постоянной величины равно самой постоянной M(C)=C. 2. Постоянный множитель можно выносить за знак мат.ожидания M(CX)=CM(X). 3. Мат.ожидание произведения двух независимых С.В. равно произведению их мат.ожиданий M(XY)=M(X)M(Y). 4. Мат.ожидание суммы двух С.В. равно сумме мат. ожиданий слагаемых M(X+Y)=M(X)+M(Y). Дисперсиейдискретной С.В. называют мат.ожидание квадрата отклонения случайной величины от ее мат. ожидания: D(X)=M[X-M(X)] По определению дисперсии: D(X)=M[X-M(X)] Дисперсия равна разности между мат. ожиданием квадрата С.В. X и квадратом ее мат. ожидания. D(X)=M(X D(X)=M[X-M(X)] Дисперсией непрерывной случайной величины называют мат.ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [a; b], то D(X)= (a и b могут быть
Свойства дисперсии: 1. Дисперсия постоянной величины C равна 0 D(C)=0. 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D(CX)= C 3. Дисперсия суммы(разности) двух независимых С.В. равна сумме(разности) дисперсий этих величин D(X  4. D(X)=M(X D(X)=M[X-M(X)] Вычисление мат.ожидания и дисперсии при биномиальном распределении.
– число появления события A в n независимых опытах. P(A)=p; q=1-p; X{0, 1, 2,…, n}, /////////////////////на всякий случай вывод для тех, кому очень интересно Формула распределения: P (m) =
По определению, математическое ожидание случайной величины вычисляется по формуле:
где x i - значения случайной величины x , p i - вероятности событий Для закона распределения случайной величины мы получим:
Поскольку
то
Окончательно:
Для дисперсии, по определению, имеем:
получим:
///////////////////////////////////////////////////////////////
p Вычисление мат. ожидания и дисперсии при распределении Пуассона. X – число появлений события A в n независимых испытаниях.
///////////////////////////////////////////////////////////// на всякий случай вывод для тех, кому очень интересно
Рассмотрим второй случай асимптотического приближения биномиального распределения, когда
В биномиальном распределении величина
Таким образом, в распределении Пуассона величина Проведем вычисления дисперсии для распределения Пуассона:
поскольку
Таким образом, в распределении Пуассона дисперсия также равна
/////////////////////////////////////////////////////////// P |
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 349. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ,…,
,…,  и выберем в каждом из них произвольную точку x
и выберем в каждом из них произвольную точку x  (i=1, 2,…, n). Определим мат. ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x
(i=1, 2,…, n). Определим мат. ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x  :
:  .
.
 ; M(X)=
; M(X)=  .
.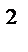 .
. -M(X)]
-M(X)]  -M(X)]
-M(X)]  p
p 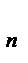 -M(X)]
-M(X)] 
 и -
и - 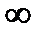 соответственно)
соответственно)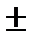 Y)=D(X)
Y)=D(X)  D(Y).
D(Y).


 .
.
 ,
,

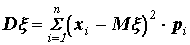 .
.
 p
p  q
q  . M(x)=np. D(x)=npq.
. M(x)=np. D(x)=npq. , а
, а  – имеет конечное значение. Случайная величина
– имеет конечное значение. Случайная величина  называется распределенной по закону Пуассона с параметром
называется распределенной по закону Пуассона с параметром  , если эта случайная величина может принимать значения
, если эта случайная величина может принимать значения  , соответствующая вероятность которых определяется по формуле Пуассона, когда
, соответствующая вероятность которых определяется по формуле Пуассона, когда  .
. имеет смысл математического ожидания. Проведем вычисления математического ожидания для распределения Пуассона:
имеет смысл математического ожидания. Проведем вычисления математического ожидания для распределения Пуассона: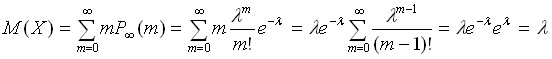 .
.

 ,
, ,
,


 ;
; 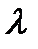 – параметр распределения;
– параметр распределения;  =np; M(x)= D(X)=
=np; M(x)= D(X)=