
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Степенные ряды. Первая теорема Абеля. Параметры и радиус сходимости. Равномерная сходимость степенного ряда. Непрерывность суммы. Почленная дифференцируемость. Ряд Тейлора.Стр 1 из 32Следующая ⇒ Непрерывность действительной функции одного действительного переменного. Определение непрерывности функции в точке. Непрерывность суммы и произведения непрерывных функций. Свойства функций, непрерывных на отрезке: теорема Вейерштрасса, теорема Больцано-Коши; непрерывность многочленной и рациональной функции. Функция называется непрерывной на некотором множестве (например, на отрезке), если она непрерывна во всех точках этого множества. Причем графически непрерывность функции, например на отрезке, означает непрерывность кривой, являющейся графиком этой функции. Рассмотрим функцию f(x), определенную в некотором интервале (
Определение непрерывности y=f(x) в точке а: при f(x) непрерывна в точке a справа, если f(x) определена на [a; a+ f(x) непрерывна в точке a слева, если f(x) определена на (a- Следовательно можно сказать, что функция непрерывна в точке а, если она в ней непрерывна справа и слева:
Непрерывность суммы, разности, произведения и частного непрерывных функций: Пусть f(x) и g(x) непрерывны и Если f(x) и g(x) обе непрерывны в точке a, то в этой же точке непрерывна их сумма, их разность, их произведение; частное непрерывно там, где знаменатель не равен 0. Свойства функций, непрерывных на отрезке: Если функция непрерывна на отрезке, то она ограничена на нем. 2. Теорема Вейерштрасса: Пусть f(x) непрерывна на отрезке [a;b]. Тогда
Следствие: если функция непрерывна на отрезке, то она достигает наибольшего и наименьшего значения на нем. 3. Теорема Больцано-Коши:  Пустьf(x) непрерывнанаотрезке [a;b], f(a) = A, f(b) = B, A Тогда Следствие: если функция непрерывна на отрезке, то она принимает все значения на нем. Прим.: теорема не утверждает, что точка Непрерывность многочленной и рациональной функции: Т.к. произведение непрерывных функций есть функция непрерывная, отсюда следует непрерывность любого одночленного выражения ax Непрерывность многочлена (целой рациональной функции) a Частное двух многочленов (дробная рациональная функция) также будет непрерывно при каждом значении x, кроме тех, которые обращают знаменатель в 0. Терема о среднем для действительных функций одного действительного переменного. Теорема Ферма; теорема Ролля; теорема Лагранжа. Примеры показывающие существенность каждого условия в теореме Роля; геометрическая интерпретация. Теорема о среднем – совокупность: Т. Ферма, Т. Роля, Т. Коши, Т. Лагранжа. Теорема Ферма: Пусть функция Доказательство: Пусть, для определенности, в точке Пусть мы подходим к точке
Делая предельный переход Пусть мы подходим к точке
Делая предельный переход Сопоставляя соотношения (1) и (2), приходим к заключению, что Аналогично для наименьшего значения. Теорема Ролля: Пусть: 1) функция f(x) определена и непрерывна на замкнутом промежутке [a; b]; 2) 3) на концах промежутка функция принимает равные значения Тогда Доказательство: f(x) непрерывна в замкнутом промежутке [a; b], поэтому
Рассмотрим 2 случая: 1) M=m. Тогда f(x) в промежутке [a; b] сохраняет постоянное значение. Производная const равна 0. 2) Оба эти значения функцией достигаются, но, т.к. f(a) = f(b), то они не могут оба достигаться на концах промежутка и хоть одно из них достигается в некоторой точке между a и b (Если, к примеру, Замечание: теорема Ролля не утверждает, что такая точка одна. На геометрическом языке теорема Роля означает следующее: если крайние кординаты кривой y=f(x) равны, то на кривой найдется точка, где касательная параллельна оси x.
Примеры показывающие существенность условий - в доказательстве (без всех условий теорема не доказуема). Теорема Лагранжа. Пусть: 1) f(x) определена и непрерывна на замкнутом промежутке [a; b], 2) f(x) дифференцируема на (a; b). Тогда Доказательство: Введем вспомогательную функцию F(x), определив ее в промежутке [a; b] равенством: Эта функция непрерывна на [a; b], т.к. представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (a; b) она имеет определенную конечную производную, равную
Подстановкой можно убедиться, что F(a)=F(b)=0, т. е. F(x) принимает равные значения на концах промежутка. Следовательно, по теореме Ролля, на интервале (a; b) существует
Степенные ряды. Первая теорема Абеля. Параметры и радиус сходимости. Равномерная сходимость степенного ряда. Непрерывность суммы. Почленная дифференцируемость. Ряд Тейлора. Степенные ряды. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 344. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
;  ). Функция f(x) называется непрерывной в точке a, если
). Функция f(x) называется непрерывной в точке a, если
 ,
,  :
: =>
=>  .
. ) и
) и 
 ; a] и
; a] и 
 =
= 
 ,
, 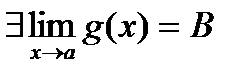 =>
=> 
 , если B
, если B  0, тогда
0, тогда 



 B.
B. , A<
, A<  <B
<B 
 [a; b] :
[a; b] :  .
. - единственная.
- единственная. = a*
= a*  (ifF(x)=x непрерывная функция).
(ifF(x)=x непрерывная функция). x
x  + a
+ a  x
x  + … + a
+ … + a 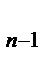 x + a
x + a 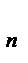 следует из непрерывности суммы непрерывных функций. В этих случаях непрерывность имеет место во всем промежутке (-
следует из непрерывности суммы непрерывных функций. В этих случаях непрерывность имеет место во всем промежутке (-  ; +
; +  ).(Сумма непрерывных функций есть непрерывная функция)
).(Сумма непрерывных функций есть непрерывная функция)

 определена и непрерывна на промежутке [a;b]и в некоторой точке
определена и непрерывна на промежутке [a;b]и в некоторой точке  этого промежутка достигает своего наибольшего и наименьшего значения, если в этой точке
этого промежутка достигает своего наибольшего и наименьшего значения, если в этой точке  , то
, то 
 функция
функция  достигает своего наибольшего. По условию теоремы эта точка внутренняя, т.е. a<x<b, и поэтому к этой точке можно подойти и справа и слева.
достигает своего наибольшего. По условию теоремы эта точка внутренняя, т.е. a<x<b, и поэтому к этой точке можно подойти и справа и слева.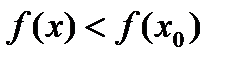 ,т.к.
,т.к.  -наибольшее значение.
-наибольшее значение. ,
,  (т.к. подходим слева) =>
(т.к. подходим слева) => 

 получим
получим  (1)
(1) (т.к. подходим справа) =>
(т.к. подходим справа) => 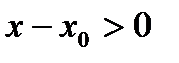

 получим
получим  (2)
(2) ;
;
 :
: 
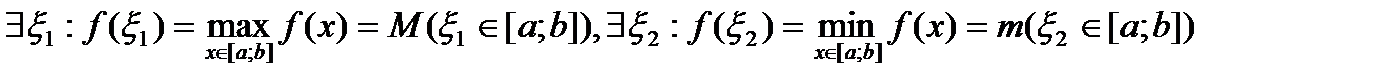 – по т.Вейрштрасса
– по т.Вейрштрасса x
x  [a; b] m<= f(x) <= M.
[a; b] m<= f(x) <= M. (M>m).
(M>m). , тогда
, тогда  , т.е. не может быть равно а). Производная в этой точке обращается в 0 ( либо
, т.е. не может быть равно а). Производная в этой точке обращается в 0 ( либо  , либо
, либо  - из т.Ферма). Теорема доказана.
- из т.Ферма). Теорема доказана.


 .
.
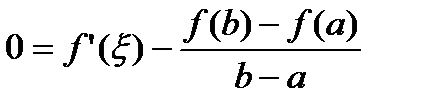 , т. е
, т. е  Теорема доказана.
Теорема доказана.