
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Центральная предельная теоремаРассмотрим другую закономерность, возникающую в результате суммарного действия случайных величин. При некоторых условиях совокупное действие случайных величин приводит к определенному, а именно — к нормальному закону распределения.Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова. Теорема Ляпунова. Если .X В данном вопросе громоздкие, хотя и достаточно понятные доказательства теорем без к-х ответ окажется очень маленьким. Хотя по усмотрению, можете обойтись перечислением теорем если не успеваете. Проверка статистических гипотез: принципы практической уверенности, статистическая гипотеза и общая схема её проверки, основная и альтернативная гипотезы, простая и сложные гипотезы, ошибки первого и второго ряда при проверке гипотезы, мощность критерия Пусть имеется некоторая выборка  Если рассматривается всего 2 взаимоисключающие гипотезы, то одну из них принято называть основной (нулевой) и обозначать При проверке статистических гипотез используется принцип практической уверенности: «если вероятность события А в данном опыте весьма мала, то можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление; если же вероятность события близка к 1, то можно предполагать, что оно достоверно произойдет». Таким образом, при правильном выборе допустимого отклонения вероятности правильного решения о принятии или не принятии гипотезы мы можем на основании вероятностных данных делать выводы невероятностного характера (например, о свойствах случайных величин). Типовые постановки задачи при проверке статистических гипотез: 1) 2) Простая основная гипотеза 3) Сложная основная гипотеза 4) Гипотеза однородности: имеется несколько выборок 5) Гипотеза независимости: наблюдается пара случайных величин 6) Гипотеза случайности: наблюдается Пусть имеются гипотезы Пусть рассматриваются две простые гипотезы
Вероятность ошибки первого рода: ////////////////////////////////////////////// Пусть дана выборка
где H0 — нулевая гипотеза, а H1 — альтернативная гипотеза. Предположим, что задан статистический критерий
сопоставляющий каждой реализации выборки Распределение Распределение Распределение Распределение Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
//////////////////////////////////////////////////////////////////// Мощностью критерия Несмотря на разнообразие самих гипотез и применяемых критериев, их можно объединить в следующую общую логическую схему: 1. Выдвижение гипотез 2. Выбор уровня значимости 3. Выбор критерия 4. Определение критической области 1 – область неправдоподобно малых 2 – правдоподобных 3 – неправдоподобно больших 5. Определение на основе выборочных данных 6. Выработка решения. Если Пусть Тогда мощность критерия
Линейные пространства. Определение, примеры, простейшие свойства. Единственность нейтрального, единственность противоположного элемента. Линейная зависимость. Координаты векторов и их связь при переходе к другому базису.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 374. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||
 , X
, X  ,…, X
,…, X 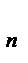 независимые С.В, у каждой из к-х существует мат. ожидание M(X
независимые С.В, у каждой из к-х существует мат. ожидание M(X  )=a, дисперсия D(X
)=a, дисперсия D(X 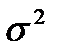 , абсолютный центральный момент третьего порядка M(|X
, абсолютный центральный момент третьего порядка M(|X 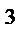 )=m
)=m  . (80) , то закон распределения суммы Y
. (80) , то закон распределения суммы Y 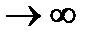 неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием  и дисперсией
и дисперсией  .
.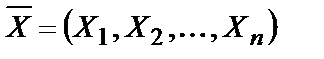 значений случайной величины
значений случайной величины  , функция распределения которой неизвестна. Статистической гипотезой
, функция распределения которой неизвестна. Статистической гипотезой  называется любое предположение о распределении наблюдений, например, предположение о том, что функция распределения
называется любое предположение о распределении наблюдений, например, предположение о том, что функция распределения  совпадает с некоторой наперед заданной функцией
совпадает с некоторой наперед заданной функцией 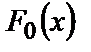 :
:  (такая гипотеза называется простой), или о том, что функция распределения принадлежит некоторому параметрическому семейству распределений
(такая гипотеза называется простой), или о том, что функция распределения принадлежит некоторому параметрическому семейству распределений  :
:  (сложная статистическая гипотеза).
(сложная статистическая гипотеза). , а другую – альтернативной (противоположной), она обозначается
, а другую – альтернативной (противоположной), она обозначается  . Обычно за
. Обычно за  принимается такая гипотеза, отвержение которой, когда она на самом деле верна, будет иметь наихудшие последствия по сравнению с теми, когда за
принимается такая гипотеза, отвержение которой, когда она на самом деле верна, будет иметь наихудшие последствия по сравнению с теми, когда за  выбирается другая гипотеза.
выбирается другая гипотеза. ; другие предположения невозможны.
; другие предположения невозможны. и сложная альтернатива
и сложная альтернатива  .
. и сложная альтернатива
и сложная альтернатива  .
.
 случайных величин
случайных величин 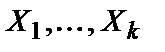 с распределениями
с распределениями  соответственно. Рассматриваются сложная основная гипотеза
соответственно. Рассматриваются сложная основная гипотеза 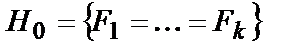 и альтернатива
и альтернатива  .
. , имеем выборку
, имеем выборку  . Рассматриваются сложная основная гипотеза
. Рассматриваются сложная основная гипотеза  и альтернативная ей гипотеза
и альтернативная ей гипотеза  .
. случайных величин
случайных величин 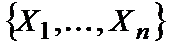 . Рассматривается сложная основная гипотеза
. Рассматривается сложная основная гипотеза 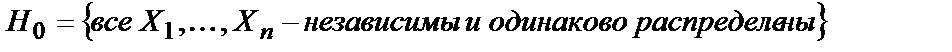 и альтернативная ей гипотеза
и альтернативная ей гипотеза 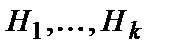 . Тогда статистическим критерием называется правило принятия одной из этих гипотез на основании имеющейся выборки, то есть отображение
. Тогда статистическим критерием называется правило принятия одной из этих гипотез на основании имеющейся выборки, то есть отображение  . Для заданного критерия
. Для заданного критерия  будем говорить, что произошла ошибка
будем говорить, что произошла ошибка  -го рода, если гипотеза
-го рода, если гипотеза  была отвергнута критерием в то время как она верна. Тогда вероятность ошибки
была отвергнута критерием в то время как она верна. Тогда вероятность ошибки  равна
равна  .
.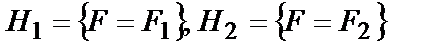 . Тогда критерием будет отображение
. Тогда критерием будет отображение  , делящее
, делящее  на два подмножества
на два подмножества  (критическая область) и
(критическая область) и  :
:
 .
. из неизвестного совместного распределения
из неизвестного совместного распределения  , и поставлена бинарная задача проверки статистических гипотез:
, и поставлена бинарная задача проверки статистических гипотез:
 ,
, одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации: соответствует гипотезе H0, и она точно определена статистическим критерием, то есть
соответствует гипотезе H0, и она точно определена статистическим критерием, то есть  .
. .
. .
.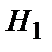 .
.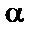 – вероятности ошибки первого рода. Эту величину называют также размером критерия. Выбор величины
– вероятности ошибки первого рода. Эту величину называют также размером критерия. Выбор величины  зависит от размера потерь, которые мы понесем в случае ошибочного решения.
зависит от размера потерь, которые мы понесем в случае ошибочного решения. . Значение критерия является случайной величиной и в предположении справедливости нулевой гипотезы
. Значение критерия является случайной величиной и в предположении справедливости нулевой гипотезы  .
.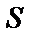 исходя из следующего условия:
исходя из следующего условия:  . Из таблиц распределения
. Из таблиц распределения  и уровня
и уровня 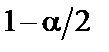 , соответственно равные
, соответственно равные  и
и 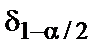 . Они разделяют всю область возможных значений случайной величины
. Они разделяют всю область возможных значений случайной величины  на три части:
на три части: ,
, ,
, значений в условиях справедливости нулевой гипотезы
значений в условиях справедливости нулевой гипотезы 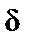 находят лишь одну квантиль: либо
находят лишь одну квантиль: либо  , либо
, либо  которая будет разделять весь диапазон значений
которая будет разделять весь диапазон значений  на две части.
на две части. численной величины статистики
численной величины статистики  , то гипотезу
, то гипотезу  рекомендуется отклонить, в противном случае ее можно принять, т.к. имеющиеся данные не противоречат высказанной гипотезе.
рекомендуется отклонить, в противном случае ее можно принять, т.к. имеющиеся данные не противоречат высказанной гипотезе. ,
,  - плотности распределения критической статистики соответственно при справедливости нулевой гипотезы
- плотности распределения критической статистики соответственно при справедливости нулевой гипотезы  ,
,  ,
,  - параметры распределения при
- параметры распределения при  . Тогда ошибки первого и второго рода определяются выражениями
. Тогда ошибки первого и второго рода определяются выражениями 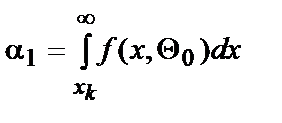 и
и  где
где  - граница критической области
- граница критической области  .
. .
.