
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон распределения дискретной С.В..P Сумма вероятностей всех значений равна 1. Законом распределения С.В. называется любое правило (таблица, функция), устанавливающее связь между возможными значениями С.В.(X) и соответствующими вероятностями. Для непрерывной С.В. – правило, функция. (табл. быть соответственно не может в силу непрерывности). Законы – F(x), f(x). Функция распределения вероятности. F(x) Функцией распределения С.В. X называется вероятность того, что она примет значения, меньшие, чем x: F(x)=P(X<x). Свойства функции распределения. 1) Функция распределения есть неубывающая функция своего аргумента. x 2) F(- 3) F(+ 4) Функция распределения есть неотрицательная функция 0<=F(x)<=1. 5) Вероятность появления случайной величины в интервале ( 6) Непрерывна слева 7) Функция распределения дискретной С.В. разрывна и возрастает скачками. (графически выглядит как лестница) 8)Непрерывна для непрерывной С.В. Плотность распределения вероятности. f(x) Плотность характеризует распределение только непрерывной С.В.. Будем считать С.В. непрерывной, если ее функция распределения дифференцируема. P(x<X<x+
f(x) = F’(x). Плотность распределения С.В.– производная ее функции в данной точке. Плотность указывает на то, как часто появляется С.В. X в некоторой окрестности точки x при повторении опытов. Св-ва: 1)F(x) = 3)f(x) Числовые характеристики С.В.. Мат. ожиданиемдискретной С.В. называют сумму произведений всех ее возможных значений на их вероятности.  Пусть X принимает значения x M(X)=x |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 341. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =P(X=x
=P(X=x  =P(X=x
=P(X=x 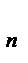 =P(X=x
=P(X=x  )=0.
)=0. )=1.
)=1. ;
; 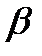 ) равна разности значений функции распределения в концах интервалов. P(
) равна разности значений функции распределения в концах интервалов. P(  <=x<=
<=x<=  x) = F(x+
x) = F(x+  x) – F(x).
x) – F(x). ;
; 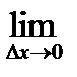
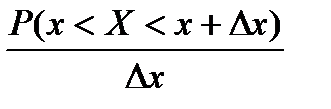 =
= 
 =F’(x).
=F’(x). 2)F(+
2)F(+ 

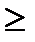 0 4) P(a<X<b) =
0 4) P(a<X<b) = 
 , x
, x  ,…, x
,…, x  , вероятности к-х соответственно равны p
, вероятности к-х соответственно равны p 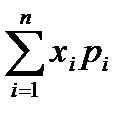 .
.