
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Введём понятие степенного рядаСтепенным рядом называется функциональный ряд с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + … члены которого есть произведения постоянных с0, с1, с2, …, сn, … на степенные функции с целыми показателями степеней от разности (z - z0). Степенной ряд с центром в точке
Введём понятие функционального ряда Пусть существует последовательность функций f0(x), f1(x), …, fn(x), … . Функциональным рядом будем называть выражение вида f0(x) + f1(x) + … + fn(x) + … . Теорема Абеля. 1)Пусть степенной ряд (1) сходится в точке 2)Если степенной ряд (1) расходится в точке Доказательство: Необходимый признак сходимости ряда (Не является достаточным): По условию, ряд Ряд (1) запишем в виде Учитывая неравенства (2) найдем Здесь Если же zрассматривать только из замкнутого круга Пусть теперь ряд (1) расходится в точке  Параметры и радиус сходимости Сходимость:пусть есть ряда1+а2+…+аn+… Егочастичныесуммы: S1=a1, S2=a1+a2 , …,Sn= a1 +….+ an .Ряд сходится if Из теоремы Абеля можно сделать заключение о характере области сходимости степенного ряда. Точка z=0 всегда лежит в области сходимости ряда (1). Если область сходимости отлична от одной точки z=0 и от всей плоскости (z), то существует круг радиуса R, называемый кругом сходимости степенного ряда(1), в каждой точке которого ряд (1) сходится абсолютно, а вне точек круга расходится.
Для определения радиуса круга сходимости используется либо признак Даламбера, либо признак Коши. Для каждого фиксированного zрассмотрим числовой ряд Т.о., для определения радиуса круга сходимости степенного ряда получаем формулу Если же к ряду (3) применим признак Коши то получим равенство
Радиус сходимости степенного ряда - Rcx= Критерий равномерной сходимости. Для того, чтобы функциональный ряд(в частности степенной ряд) сходился равномерно в области D, необходимо и достаточно, чтобы
Абсолютная сходимость: ряд а1+а2+…+аn+… сходится абсолютно, если сходится ряд |а1 |+|а2 |+…+|аn|+… Непрерывность суммы Свойство степенных рядов. Сумма степенного ряда есть функция, непрерывная на интервале сходимости ряда. S(z) = z0 + a1z + a2z2 + … + anzn + … Причём, в том конце интервала, где степенной ряд сходится, его сумма S(x) остаётся односторонне непрерывной. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 354. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 :
:  , где D –область.
, где D –область.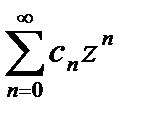 - ряд с центром в точке z0 = 0 (1)
- ряд с центром в точке z0 = 0 (1) .Тогда он сходится абсолютно в любой точке z, для которой |
.Тогда он сходится абсолютно в любой точке z, для которой | 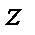 |<|
|<| 
 , тогда он расходится и во всех точках z таких, что |z|>|
, тогда он расходится и во всех точках z таких, что |z|>| 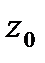 |.
|. при
при 
 сходится, следовательно,
сходится, следовательно,  . Любая последовательность, имеющая предел, ограничена, значит, существует такое число M:
. Любая последовательность, имеющая предел, ограничена, значит, существует такое число M:  для всех n=0, 1,… (2)
для всех n=0, 1,… (2)
 , т.к.
, т.к. 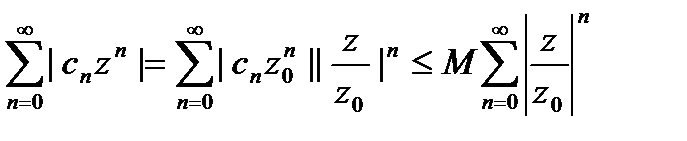 .
. , поэтому последний ряд сходится, а это означает, что сходится ряд
, поэтому последний ряд сходится, а это означает, что сходится ряд 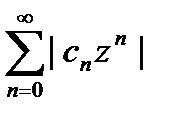 , т. е. при |z|<|| исходный степенной ряд (1) сходится абсолютно.
, т. е. при |z|<|| исходный степенной ряд (1) сходится абсолютно.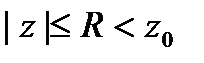 , то
, то 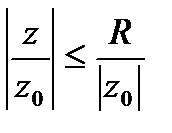 , а это означает, что степенной ряд (1) мажорируется сходящимся числовым рядом
, а это означает, что степенной ряд (1) мажорируется сходящимся числовым рядом 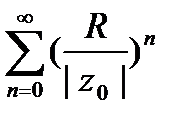 и по признаку Вейерштрасса исходный степенной ряд (1) сходится равномерно в круге
и по признаку Вейерштрасса исходный степенной ряд (1) сходится равномерно в круге  . Предположим, что в точке
. Предположим, что в точке  такой, что |
такой, что |  |>|
|>|  | ряд (1) сходится. Тогда по предыдущему утверждению ряд (1) сходится и в точке
| ряд (1) сходится. Тогда по предыдущему утверждению ряд (1) сходится и в точке 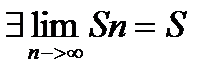 , где S конечно.
, где S конечно.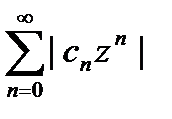 (3) и применим к нему признак Даламбера. Именно: если существует предел
(3) и применим к нему признак Даламбера. Именно: если существует предел 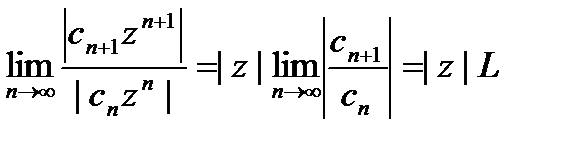 (4) , то ряд (3) сходится, если
(4) , то ряд (3) сходится, если  и расходится, если
и расходится, если 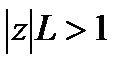 . Отсюда заключаем, что если выполнено соотношение
. Отсюда заключаем, что если выполнено соотношение 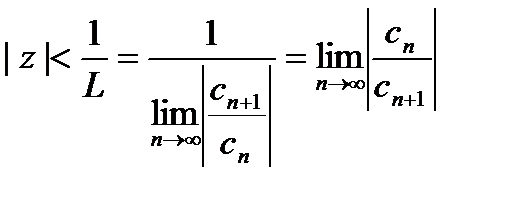 , то ряд (3) сходится абсолютно, а если имеет место неравенство
, то ряд (3) сходится абсолютно, а если имеет место неравенство 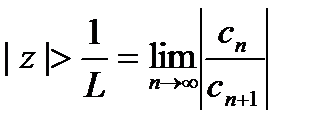 , то ряд (1) как и ряд (3), расходится.
, то ряд (1) как и ряд (3), расходится. (5).
(5). 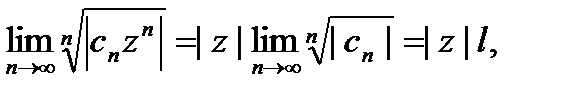 из которого заключаем, что ряд (3) сходится, если
из которого заключаем, что ряд (3) сходится, если  , и расходится, если
, и расходится, если  . Т.о., радиус круга сходимости Rряда (1) определяется по формуле
. Т.о., радиус круга сходимости Rряда (1) определяется по формуле  . (6) (формула Коши — Адамара.)
. (6) (формула Коши — Адамара.)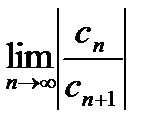 =
= 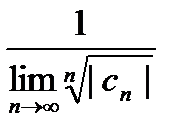
 и
и 
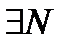 : при n>N
: при n>N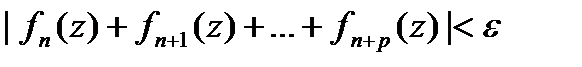 , p =0,1,2,3,…
, p =0,1,2,3,…