
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Почленная дифференцируемостьТеорема1:. Cтепенной ряд внутри интервала сходимости (|z|<R) имеет сумму S(x), к-я дифференцируема сколь угодно много раз. Степенной рядможно почленно дифференцировать любое число раз, причем радиус круга сходимости продифференцированных рядов также равен R. S(x)= с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + … S’(x)= с1 + с2 *2*(z – z0) + … + сn*n*(z – z0)n-1 + … Ряд Тейлора Имеем степенной ряд
Первообразная и неопределённый интеграл. Определение первообразной. Определение неопределённого интеграла, его свойства. Определение интеграла по Риману. Необходимые и достаточные свойства интегрируемости. Формула Ньютона-Лейбница. Пусть определены функции f(x) и F(x). F(x) – первообразная f(x), если F’(x) = f(x). F(x) + c – тоже первообразная f(x). Неопределенный интеграл: Свойства неопределенного интеграла: 1) 2) d 3) 4)
Определение интеграла по Риману Пусть функция y=f(x) определена на отрезке [a; b], a<b. Выполним следующие действия: 1. С помощью точек 2. В каждом частичном отрезке [ 3. Умножим найденное значение функции  4.Сост. сумму S
Сумма вида (1) называется интегральной суммой функции y=f(x) на отрезке [a; b]. Обозначим через 5. Найдем предел интегральной суммы (1), когда n Если при этом интегральная сумма Необходимые и достаточные условия интегрируемости Введём понятие верхней и нижней суммы Дабру. Пусть функция f(x) определена на отрезке [a; b], S Сумма S Теорема. Для того чтобы ограниченная на некотором отрезке функция была интегрируема на нем, необходимо и достаточно, чтобы суммы Дарбу S Следствие. Для того чтобы ограниченная на отрезке [a; b] функция f была на нем интегрируема, необходимо и достаточно, чтобы где Формула Ньютона-Лейбница Пусть функция y=f(x) интегрируема на отрезке [a; b]. Теорема.Если функция y=f(x) непрерывна на отрезке [a; b] и F(x) - какая-либо ее первообразная на [a; b] (F’(x)=f(x)), то имеет место формула Доказательство: Пусть на отрезке [a;b] задана интегрируемая функция f(x). Зададим произвольное значение
Основные понятия теории вероятности: классификация событий. Классические определения вероятности. Геометрические определения вероятности. Теоретико-множественная трактовка основных понятий и аксиоматическое построение теории вероятности. Теорией вероятности наз. мат. наука, изучающая закономерности в случайных событиях. Классификация событий: Событие– всякий факт, который может произойти в результате некоторого опыта. Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий. Его вероятность равна 1 (P=1). Невозможнымназывают событие, которое заведомо не произойдет, если будет осуществлена совокупность условий. Его вероятность равна 0 (P=0). Случайное событие – такое событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти (0<P<1). Два события называются совместными, если появление одного из них не исключает появления другого. Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании. Противоположные события –событие А называют противоположным B, если результат его противоположен результату B. P(A) + P(B) =1 Классическое определение вероятности: вероятность есть число, характеризующее степень возможности появления события. Каждый возможный результат – элементарный исход. Те элементарные исходы, в кот.интересующее нас событие наступает, называются благоприятствующими исходами. Т.о., событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих А. Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. P(A)= n – число всех возможных элементарных исходов. Недостаток классического определения вероятности – оно неприменимо к испытаниям с бесконечным числом исходов. Для преодоления этого недостатка вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т. д.). Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l определяется равенством: P= Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством: P= |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 356. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
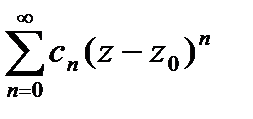 . Обозначим через f(z) его сумму. Сходится в круге |z -
. Обозначим через f(z) его сумму. Сходится в круге |z -  |<R.
|<R.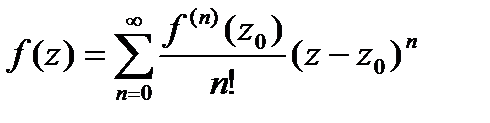 называется рядом Тейлора функции f(z) по степеням (z-
называется рядом Тейлора функции f(z) по степеням (z- 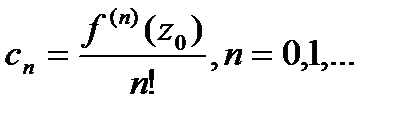 - эти выражения называются коэффициентами Тейлора функции f(z) в точке
- эти выражения называются коэффициентами Тейлора функции f(z) в точке 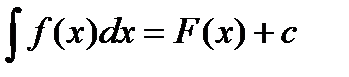 - множество всех первообразных f(x).
- множество всех первообразных f(x).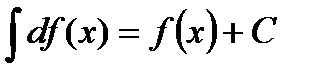
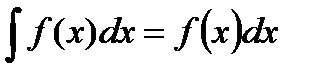
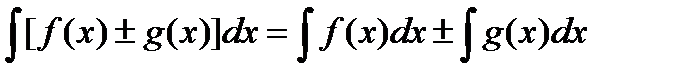
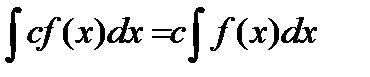 , где с – const
, где с – const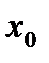 =a,
=a, 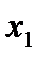 ,
, 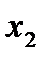 ,…,
,…, 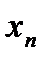 =b (
=b ( 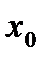 <
< 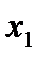 <
< 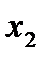 <…<
<…< 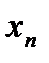 ) разобьем отрезок [a; b] на n частичных отрезков [
) разобьем отрезок [a; b] на n частичных отрезков [ 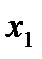 ], [
], [ 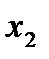 ],…, [
],…, [ 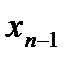 ,
, 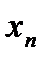 ]
] 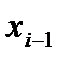 ,
, 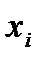 ], i=1, 2,…, n выберем произвольную точку c
], i=1, 2,…, n выберем произвольную точку c 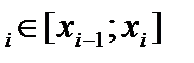 и вычислим значение функции в ней, т. е. величину
и вычислим значение функции в ней, т. е. величину 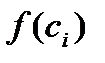 .
.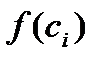 на длину
на длину 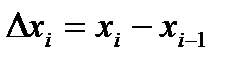 соответствующего частичного отрезка:
соответствующего частичного отрезка: 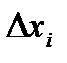 .
.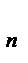 всех таких произведений.:
всех таких произведений.: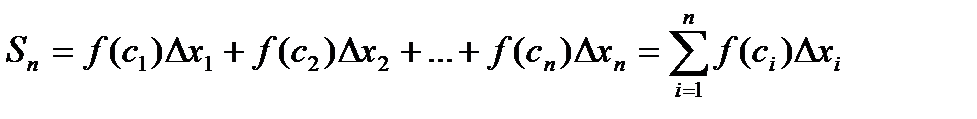 (1)
(1)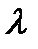 длину наибольшего частичного отрезка
длину наибольшего частичного отрезка 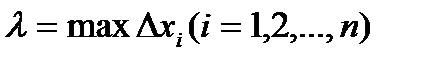 .
.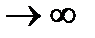 так, что
так, что 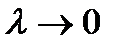 .
.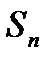 имеет предел I, который не зависит ни от способа разбиения отрезка [a; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции y=f(x) на отрезке [a,b]
имеет предел I, который не зависит ни от способа разбиения отрезка [a; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции y=f(x) на отрезке [a,b] 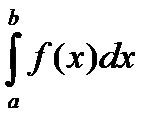 Т.о.,
Т.о., 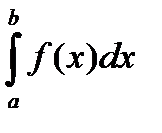 =
= 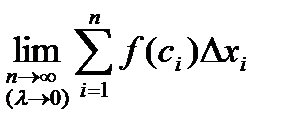 (2)
(2)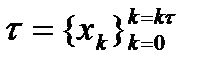 разбиение этого отрезка
разбиение этого отрезка 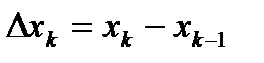 . Положим
. Положим 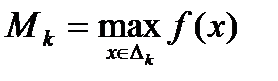 (т.е. Mk максимальное значение функции на отрезке [k-1;k]), m
(т.е. Mk максимальное значение функции на отрезке [k-1;k]), m 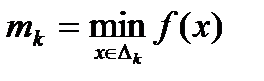 (mk - минимальное), k=1, 2,…, k
(mk - минимальное), k=1, 2,…, k  (3)
(3) = S
= S  (f)=
(f)= 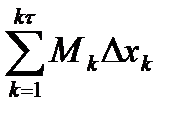 , s
, s  = s
= s  (f)=
(f)= 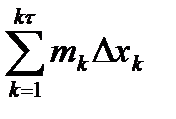 . (4)
. (4)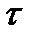 называется верхней, а сумма s
называется верхней, а сумма s 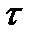 - нижней суммой Дарбу функции f. В случае, когда функция f ограничена, то нижние
- нижней суммой Дарбу функции f. В случае, когда функция f ограничена, то нижние 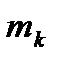 и верхние
и верхние 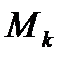 грани (3) конечны, и потому суммы Дарбу (4) при любом разбиении принимают конечные значения.
грани (3) конечны, и потому суммы Дарбу (4) при любом разбиении принимают конечные значения.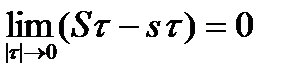 (5)
(5)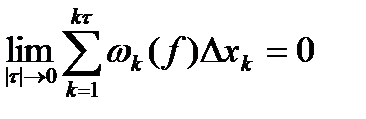 (6)
(6)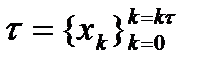 - разбиение отрезка [a; b], а
- разбиение отрезка [a; b], а 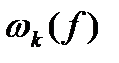 - колебание функции f на отрезке
- колебание функции f на отрезке 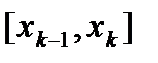 , k=1, 2,…, k
, k=1, 2,…, k  .
.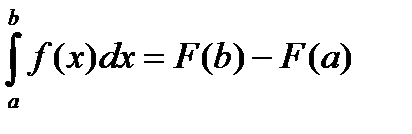
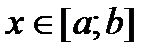 . Пусть функция F(x)- какая-нибудь первообразная для заданной функции f(x). Тогда она может быть получена по формуле
. Пусть функция F(x)- какая-нибудь первообразная для заданной функции f(x). Тогда она может быть получена по формуле 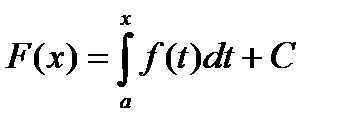 .Таким образом, учитывая, что C=F(a), имеем:
.Таким образом, учитывая, что C=F(a), имеем: 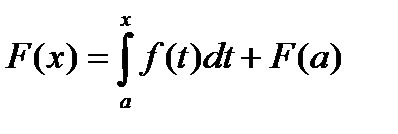 . Пологая теперь x=b получаем:
. Пологая теперь x=b получаем: 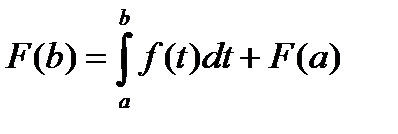 . Откуда:
. Откуда: 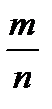 , m – число элементарных исходов, благоприятствующих А;
, m – число элементарных исходов, благоприятствующих А;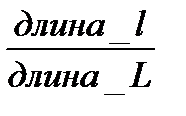 .
.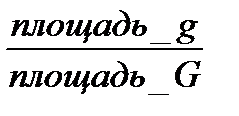 .
.