
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнения и вычеты. Кольцо вычетов. Малая терема Ферма. Сравнения первой степени. Китайская теорема об остатках.Сравнения Зафиксируем натуральное число т =>1, которое условимся называть модулем. Определение 1. Два целых числа а, bназовем сравнимыми по модулю т, если они при делении на т дают одинаковые остатки. Обозначение: Рассмотрим простейшие свойства сравнений. Сравнения первой степени – с-ва Теорема 1.Сравнения целых чисел по модулю т обладают следующими свойствами для любых а, b, с, d€ Z: (т. е. сравнения можно почленно складывать, вычитать и перемножать), 6) если d есть общий делитель чисел а, b, т, то 7) если числа а, b делятся на d и d взаимно просто с т, то Классы вычетов по модулю т Из свойств 1) — 3) сравнений видно, что отношение сравнимости целых чисел по модулю т является отношением эквивалентности, и, следовательно, множество целых чисел разбивается на непересекающиеся классы сравнимых по модулю m чисел. Так как различные остатки при делении на т исчерпываются числами 0,1,2,...,m-1, то получим т классов: Классы (2) называются классами вычетов, а их элементы — вычетами по модулю т. Из определения сравнений следует, что числа из одного класса сравнимы по модулю т, а числа из разных классов не сравнимы по модулю т, т. е. Определение 1. Совокупность чисел, взятых по одному из каждого класса вычетов по модулю т, называется полной системой вычетов по модулю т. Примером полной системы вычетов по модулю т является множество чисел 0,1,... , m — 1. Это так называемая полная система наименъшцх неотрицательных вычетов. 
Cледующее свойство полных систем вычетов. Теорема 1.Если Доказательство (можно не писать – М.С.). Все числа ряда (3) принадлежат разным классам вычетов по модулю т, поскольку в силу свойств сравнений Малая терема Ферма Теорема. Если натуральные числа а, т взаимно просты, то
Следствие. Если р — простое число и
Для доказательства утверждения а) достаточно заметить, что
Заметим, что утверждение а) следствия впервые доказал Ферма, оно называется малой теоремой Ферма. Теорема б была позднее доказана Эйлером и носит название теоремы Эйлера — Ферма. Она находит широкое применение в математике и ее приложениях и, в частности, может оказаться полезной при нахождении остатков от деления степеней числа на заданное число, при решении сравнений с неизвестными и т. д. Кольцо вычетов Рассмотрим множество Следовательно, классы вычетов по модулю та совпадают со смежными классами кольца Z по его идеалу mZ. Теорема 1. Определение операций сложения и умножения классов вычетов по формулам
Кольцо Z/rn называют кольцом классов вычетов по модулю т. Опишем обратимые элементы этого кольца. Теорема 2.Элемент Китайская теорема об остатках Пусть m - натуральное число, m1, m2, ..., mt - взаимно простые натуральные числа, произведение которых больше либо равно m. Теорема: Любое число x: 0 <= x <= m может быть однозначно представлено в виде последовательности r(x) = (r1, r2, ..., rt), где ri = x(mod mi). Для любых чисел r1 .. rt, таким образом, существует единственное число x(mod m), такое что x = ri(mod mi), 1 <= i <= t Более того, любое решение x набора такого сравнений имеет вид x = r1*e1 + ... + rt*et (mod m), где ei = m / mi * ( ( m/mi )-1 mod mi ), 1 <= i <= t.
Системы линейного уравнения над кольцом и полем. Системы линейных уравнений над коммутативным кольцом с единицей. Равносильность систем. Системы уравнений над кольцом. Однородные уравнения и функциональная система решений.
Алгоритмы на графах. Обход графа в глубину, построение глубинного остового леса и классификация ребер, не вошедших в лес. Алгоритмы нахождения связных компонентов неориентированных графов и сильно связных компонентов ориентированных графов. Поиск в ширину и кратчайшие пути в графе. Обход в глубину— это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода): 1)Рассматриваем вершину Х.Двигаемся в любую другую, ранее непосещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину; 2) Если из вершины Хнельзя попасть в ранее непосещенную вершину или таковой нет, то возвращаемся в вершину Z, из которой впервые попали в X, и продолжаем обход в глубину из вершины Z. 3) Такой обход графа продолжается до тех пор, пока очередная вершина Х, не совпадет с вершиной Х0,с которой начался обход графа (компоненты связности). Обход в ширину — это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода): 1)Рассматриваем вершину Х. Ей присваивается метка 0; 2) Всем смежным вершинам с вершиной с меткой 0 поочередно присваиваются метки 1; 3) Всем смежным вершинам с вершинами с меткой 1 поочередно присваиваются метки 2; 4) И т.д. до тех пор, пока не будут помечены все вершины в текущем графе (компоненте связности). Связный граф Граф, в котором все вершины связаны. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 755. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


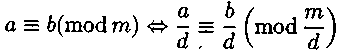

 (2)где через
(2)где через  обозначен класс всех чисел, которые при делении на т дают в остатке r. Очевидно, что класс
обозначен класс всех чисел, которые при делении на т дают в остатке r. Очевидно, что класс  однозначно определяется любым одним своим представителем, и потому в дальнейшем класс
однозначно определяется любым одним своим представителем, и потому в дальнейшем класс  будет обозначаться также в виде
будет обозначаться также в виде 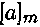 , где а — любой представитель этого класса.
, где а — любой представитель этого класса.
 есть полная система вычетов по модулю т, число а взаимно простое с т и b— любое целое число, то
есть полная система вычетов по модулю т, число а взаимно простое с т и b— любое целое число, то  (3) есть также полная система вычетов по модулю т.
(3) есть также полная система вычетов по модулю т.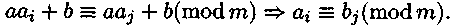 А так как в (3) содержится т чисел, т. е. столько же чисел, сколько и классов, то в (3) имеется ровно по одному представителю из каждого класса. Следовательно, (3) есть полная система вычетов по модулю т
А так как в (3) содержится т чисел, т. е. столько же чисел, сколько и классов, то в (3) имеется ровно по одному представителю из каждого класса. Следовательно, (3) есть полная система вычетов по модулю т
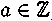 , то
, то
 . Утверждение б) при
. Утверждение б) при 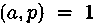 следует из а) и следствия 1 теоремы 2, а при
следует из а) и следствия 1 теоремы 2, а при  очевидно, поскольку в этом случае
очевидно, поскольку в этом случае .
. всех классов вычетов по модулю
всех классов вычетов по модулю  . Класс
. Класс  состоит из всех чисел вида
состоит из всех чисел вида  , где tпробегает множество Z, т. е.
, где tпробегает множество Z, т. е. 
 корректно, и множество
корректно, и множество  с этими операциями является коммутативным кольцом с единицей. Это есть факторкольцо
с этими операциями является коммутативным кольцом с единицей. Это есть факторкольцо  кольца Zпо его идеалу тZ.
кольца Zпо его идеалу тZ. обратим в кольце Z/mтогда и только тогда, когда класс
обратим в кольце Z/mтогда и только тогда, когда класс  взаимно прост с т, т. е. (а,т) = 1.
взаимно прост с т, т. е. (а,т) = 1.