
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление мат.ожидания и дисперсии при нормальном законе распределения.Нормальным называют распределение вероятностей непрерывной С.В., которое описывается плотностью f(x)= Нормальное распределение определяется двумя параметрами: a и M(X)=a. D(X)=
Законы больших чисел и предельные теоремы: неравенство Маркова, неравенство Чебышева, теорема Чебышева, центральная предельная теорема. Законы больших чисел и предельные теоремы Закон больших чисел (в широком смысле) – общий принцип, согласно которому, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и м.б. предсказан с большой степенью определенности. Закон больших чисел (в узком смысле) – ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. Неравенство Маркова (лемма Чебышева) Теорема.Если случайная величина X принимает только неотрицательные значения и имеет мат. ожидание, то для любого положительного числа А верно неравенство P(x>A) Доказательство: проведем для дискретной случайной величины X. Расположим ее значения в порядке возрастания, из которых часть значений x Запишем выражение для математического ожидания M(X): x  где p Отбрасывая первые k неотриц. слагаемых получим x Заменяя в неравенстве (2) значения x Сумма вероятностей в левой части полученного неравенства представляет собой, сумму вероятностей событий X=x Поэтому P(X>A) <= Неравенство Чебышева Теорема.Для любой случайной величины, имеющей мат. ожидание и дисперсию, справедливо неравенство Чебышева: P(|X-a|> Доказательство: Применим неравенство Маркова в форме (1) к случайной величине X’=(X-a) Т.к. неравенство Теорема Чебышева Если дисперсии n независимых С.В. X
Докажем формулу (5). По условию M(X Возьмем такое С: D(X Получим неравенство Чебышева для средней арифметической случайных величин, т.е. для X= M(X)=M( D(X)=D( (Здесь использованы свойства математического ожидания и дисперсии, в частности, то, что случайные величины X Применяем неравенство Чебышева(вариант Германа) для С.В - X=(X Т.к. по доказанному D(X) В пределе при n |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 364. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. . Достаточно знать эти параметры, чтобы задать нормальное распределение.
. Достаточно знать эти параметры, чтобы задать нормальное распределение.
 .
. . (1)
. (1) , x
, x  ,…, x
,…, x  будут не более числаА, а другая часть - x
будут не более числаА, а другая часть - x  ,…, x
,…, x  будут больше А, т.е.x
будут больше А, т.е.x 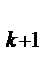 >A,…, x
>A,…, x  p
p  +…+ x
+…+ x 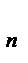 .
.  .
. )<=
)<=  , (3) где a=M(X),
, (3) где a=M(X),  >0. ( P(|X-a|
>0. ( P(|X-a| 
 1 -
1 -  взяв в качестве положительного числа A=
взяв в качестве положительного числа A=  . Получим
. Получим  <=
<= 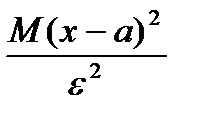 . (4)
. (4)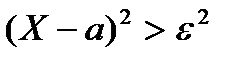 равносильно неравенству |X-a|>
равносильно неравенству |X-a|>  , а M(X-a)
, а M(X-a) 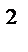 есть дисперсия случайной величины X, то из неравенства (4) получаем доказываемое неравенство (3).
есть дисперсия случайной величины X, то из неравенства (4) получаем доказываемое неравенство (3).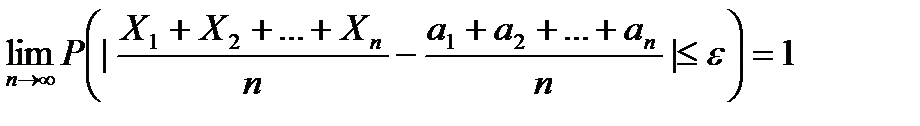 (5) или
(5) или 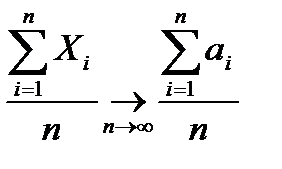 .
. )=a
)=a  )=a
)=a  )=a
)=a 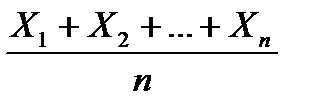 . Найдем мат. ожидание M(X) и оценку дисперсии D(X)
. Найдем мат. ожидание M(X) и оценку дисперсии D(X) )=
)=  ;
; .
. (6)
(6)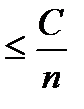 , то 1-
, то 1-  , и от неравенства (6) перейдем к более сильному неравенству:
, и от неравенства (6) перейдем к более сильному неравенству: 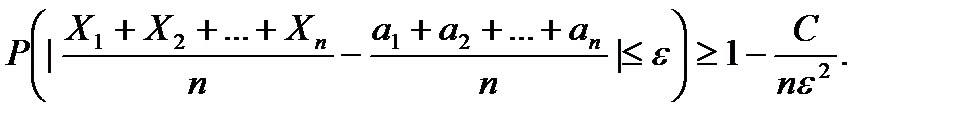 (7)
(7) величина
величина 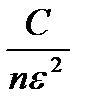 стремится к нулю, и получим доказываемую формулу (5).
стремится к нулю, и получим доказываемую формулу (5).