
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интервальные оценки параметровВыборка, полученная из генеральной совокупности, содержит n значений признака - случайной величины Х. Найденные значения точечных характеристик в свою очередь будут случайными величинами, меняющимися от выборки к выборке. Однако они используются для оценки неслучайных числовых параметров генеральной совокупности – математического ожидания (генеральной средней) и дисперсии (генеральной дисперсии). С этим обстоятельством связана необходимость ввести в рассмотрение понятия интервальных оценок параметров – оценок, определяемых двумя числами, границами некоторого интервала. Интервальной оценкой какого-либо оцениваемого параметра служит доверительный интервал. Доверительный интервал – интервал со случайными границами, вычисляемыми по выборке, который с заданной исследователем (доверительной) вероятностью «накрывает» оцениваемый параметр. Как правило, выбирается симметричный интервал относительно Пусть исследуемый признак распределен в соответствии с нормальным законом распределения. Интервальная оценка для генеральной средней: а) при известной среднеквадратической ошибке измерения:
где б) при неизвестной среднеквадратической ошибке
где s - среднее выборочное квадратическое отклонение;  Интервальная оценка для генеральной дисперсии:
где D – генеральная дисперсия k =n-1 или k=n-m; Интервальная оценка для генерального среднего квадратического отклонения:
где
Подсчитаем интервальные оценки параметров для примера 8.1. 4Зададимся доверительной вероятностью По таблице находим:
Доверительный интервал для генеральной дисперсии в соответствии с формулой (8.4.3.) :
Доверительный интервал для генерального среднего квадратического отклонения в соответствии с формулой (8.4.4.): по таблицам
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 405. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
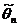 .
.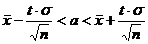 (8.4.1.),
(8.4.1.),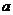 - генеральная средняя (математическое ожидание);
- генеральная средняя (математическое ожидание); 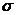 - известное среднее квадратическое отклонение; n - объем выборки; t определяется из условия
- известное среднее квадратическое отклонение; n - объем выборки; t определяется из условия 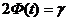 , где
, где 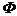 - функция Лапласа, заданная таблично;
- функция Лапласа, заданная таблично; 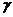 - доверительная вероятность, назначаемая исследователем.
- доверительная вероятность, назначаемая исследователем.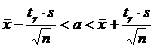 (8.4.2.),
(8.4.2.),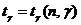 - табулированная функция, построенная на основе распределения Стьюдента.
- табулированная функция, построенная на основе распределения Стьюдента.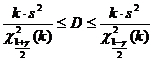 (8.4.3.),
(8.4.3.),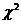 - квантили
- квантили 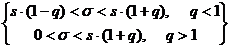 (8..4.4)
(8..4.4)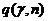 - таблично заданная функция.
- таблично заданная функция.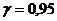 . Так как истинное значение
. Так как истинное значение 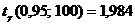 . Тогда
. Тогда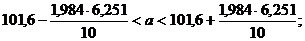 или
или 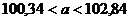 .
.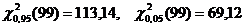 ; тогда
; тогда 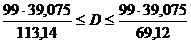 , или
, или 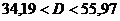 .
.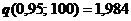 . Тогда
. Тогда 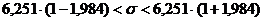 , или
, или 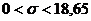 .3
.3