Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение теоретического закона распределения по опытным данным. Проверка гипотезы о законе распределенияОдной из важнейших задач математической статистики является установление теоретического закона распределения изучаемого признака по опытным данным – имеющейся выборке из генеральной совокупности. Для решения этой задачи надо определить (подобрать) вид и параметры закона распределения. Как правило, это делают при помощи гистограммы или полигона частот, так как эти графические характеристики выступают аналогом функции плотности вероятностей. Параметры закона распределения, как правило, неизвестны, поэтому их заменяют точечными оценками, находимыми по выборке. Как бы хорошо ни был подобран теоретический закон распределения, между эмпирическим и теоретическим законом неизбежны расхождения. Для ответа на вопрос: носят ли эти расхождения случайный характер, или являются следствием несоответствия подобранного закона истинному, служат критерии согласия. Наиболее часто используется критерий согласия Пирсона или В критерии согласия Пирсона проверяется статистическая гипотеза Пример 8.5. Для примера 1 по критерию Пирсона проверить гипотезу о нормальном законе распределения на уровне значимости 
3 Был получен вариационный ряд:
и построена гистограмма. Вид гистограммы позволяет предположить, что изучаемый признак распределен нормально. Теоретические значения математического ожидания Для расчета вероятностей попадания признака в интервалы
Для вычисления статистики
Число степеней свободы дисперсии
8.6. Построение теоретической кривой по методу наименьших квадратов Как правило, в экспериментах задается значение некоторой величины Х и измеряется значение некоторой другой величины У связанной с Хфункциональной зависимостью, вид которой не известен. В результате получают таблично заданную функцию Метод наименьших квадратов (МНК) позволяет построить аналитическое выражение функции Математически эта задача формулируется следующим образом:
Как правило, вид теоретической кривой выбирается в виде полинома
тогда (8.6.1.) записывается так:
В силу квадратичности функционала Lотносительно коэффициентов МНК особенно удобен для использования в матричной форме. Пусть проведен эксперимент в котором получено n пар значений Введем матрицы:
Система нормальных уравнений размерности
Разрешая это матричное уравнение относительно матрицы
При найденных таким образом коэффициентах Пример 8.6: По МНК построить теоретическую кривую в виде полинома второго порядка
Введем матрицы в соответствии с (8.6.5.):
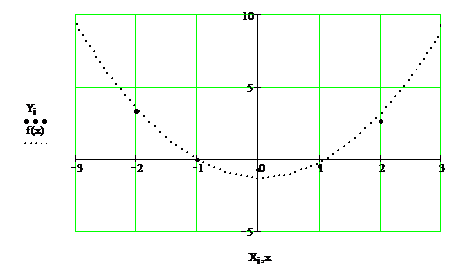
Теоретическая кривая: На рис. 8.4. приведена теоретическая кривая и показаны экспериментальные точки.
Рис. 8.4.
Задачи 8.1. Анализируются статистические данные о продажах в регионах (т. грн.):
Построить простой статистический и вариационный ряды, графические характеристики.
В последующих задачах дано распределение признака Х, полученного по наблюдениям. Необходимо: 1) построить полигон (гистограмму), эмпирическую функцию распределения; 2) найти Точечные оценки выборки: 8.2 Х – число сделок на фондовой бирже за квартал; n=400– число инвесторов.
Ответ: 8.3. Х – месячный доход жителя региона (в грн.); n=1000.
Ответ: 8.4. Х – удой коров на молочной ферме за лактационный период в ц, n=100 коров.
Ответ: В задачах 8.1 – 8.4 найти доверительные интервалы с надежностью 8.5. По данным 9 измерений некоторой величины найдены средняя результатов измерений Ответ: 8.6. Средняя квадратическая ошибка показаний альтиметра (высотомера) самолета равна 15 м. Скольно надо иметь таких приборов на самолете, чтобы с надежностью 0,9 ошибка средней высоты была больше (-30) м, если закон распределения ошибки нормальный? Ответ: Нужно иметь не менее двух приборов. 8.7. В рекламе утверждается, что месячный доход по акциям Апревышает доход по акциям Вболее чем на 0,3%. В течение годичного периода средний месячный доход по акциям Всоставил 0,5%, а по акциям А– 0,65%, а его средние квадратические отклонения составили 1, и 2,0%% соответственно. Полагая распределение доходности нормальным, с надежностью 0,95 проверить утверждение, содержащееся в рекламе. Ответ:Утверждение противоречит имеющимся данным. 8.8 Вступительный экзамен проводился на двух факультетах университета. На первом факультете из экзамен Ответ: Существенных различий нет. ( 8.9. Расход сырья на единицу продукции составил:
Считая, что расходы сырья по каждой технологии имеет тормальное распределение с одинаковыми дисперсиями, на уровне значимости Ответ: Новая технология дает экономию: ( 8.10. Ожидается, что добавление специальных веществ уменьшает жесткость воды. Оценка жесткости проведении до и после добавления веществ по 40 и 50 пробам (%): до
После
Подтверждают ли результаты этот эффект? Ответ: да ( 8.11. По данным задачи 8.10. выдвинуть гипотезу о законе распределения и проверить ее по критерию Пирсона при 8.12 По данным задачи 8.4. проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности ( 8.13. При 50 подбрасываниях монеты герб выпал 30 раз. Можно ли считать монету симметричной? (решить для Ответ: Монета несимметрична. 8.14. При 120 бросаниях игральной кости шестерка выпала 40 раз. Можно ли считать кость правильной? (решить для Ответ: кость правильная. 8.15. Методом наименьших квадратов построить теоретическую кривую заданного вида (
Ответ: 8.16. Методом наименьших квадратов построить теоретическую кривую заданного вида: (
Ответ: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 431. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
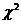 -критерий.
-критерий. 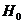 о виде теоретического закона распределения. Сравнивается с критическим значением сумма квадратов отклонений опытного числа попаданий в каждый интервал
о виде теоретического закона распределения. Сравнивается с критическим значением сумма квадратов отклонений опытного числа попаданий в каждый интервал 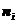 от теоретического их числа
от теоретического их числа 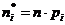 , где
, где 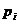 - теоретические вероятности попадания в i-й интервал значений изучаемого признака в случае действительной реализации подобранного закона распределения. Вычисляемая статистика
- теоретические вероятности попадания в i-й интервал значений изучаемого признака в случае действительной реализации подобранного закона распределения. Вычисляемая статистика 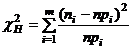 сравнивается с критическим значением
сравнивается с критическим значением 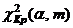 , где
, где 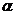 - уровень значимости,
- уровень значимости, 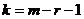 - число степеней свободы дисперсии,
- число степеней свободы дисперсии, 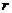 - число параметров в теоретическом законе распределения. Если
- число параметров в теоретическом законе распределения. Если 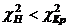 гипотеза принимается.
гипотеза принимается.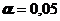 .
.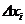
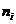
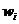
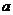 и среднего квадратического отклонения
и среднего квадратического отклонения 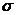 неизвестны, поэтому заменяем их «наилучшими оценками»
неизвестны, поэтому заменяем их «наилучшими оценками» 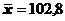 и
и 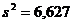 .
.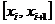 используем таблицы функций Лапласа:
используем таблицы функций Лапласа: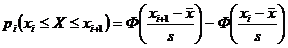 . Теоретические частоты
. Теоретические частоты 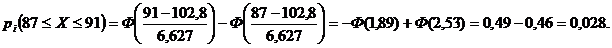
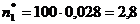
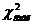 удобно пользоваться таблицей:
удобно пользоваться таблицей: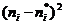
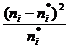
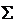
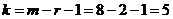 ;
;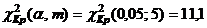 . Так как
. Так как 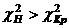 , то гипотеза о нормальном законе распределения отвергается. 4
, то гипотеза о нормальном законе распределения отвергается. 4 . Аналитический вид этой функции неизвестен.
. Аналитический вид этой функции неизвестен.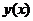 (теоретическую кривую) по опытным данным. В соответствии с МНК теоретическая кривая
(теоретическую кривую) по опытным данным. В соответствии с МНК теоретическая кривая 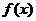 должна проходить так, чтобы сумма квадратов отклонений ее ординат от экспериментальных данных в опытных точках была минимальной.
должна проходить так, чтобы сумма квадратов отклонений ее ординат от экспериментальных данных в опытных точках была минимальной.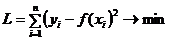 (8.6.1.).
(8.6.1.).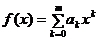 (8.6.2.),
(8.6.2.),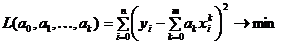 (8.6.3.).
(8.6.3.).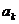 и неотрицательности существует единственный минимум. Условия экстремума Lпозволяют получить систему m уравнений для вычисления коэффициентов
и неотрицательности существует единственный минимум. Условия экстремума Lпозволяют получить систему m уравнений для вычисления коэффициентов 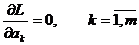 (8.6.4).
(8.6.4).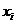 и
и 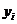 ; теоретическая кривая выбрана в виде полинома (8.6.2).
; теоретическая кривая выбрана в виде полинома (8.6.2).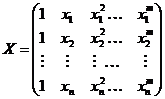 ;
; 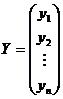 ;
; 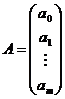 (8.6.5.).
(8.6.5.).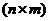 будет представлена в виде:
будет представлена в виде: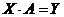
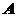 , находим:
, находим: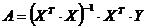 (8.6.6).
(8.6.6).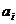 условие (8.6.3) выполнится.
условие (8.6.3) выполнится.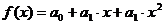 для обработки эксперимента:
для обработки эксперимента: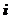
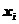
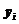
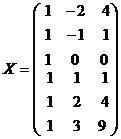 ;
; 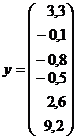 ;
; 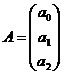 ; По (8.6.6) находим:
; По (8.6.6) находим: 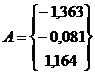 .
.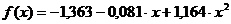 .
.
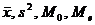 .
.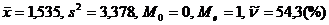
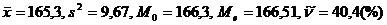
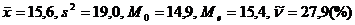
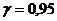 для генерального среднего, дисперсии и среднего квадратического отклонения .
для генерального среднего, дисперсии и среднего квадратического отклонения .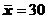 и выборочная дисперсия
и выборочная дисперсия 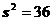 . Найти границы, в которых с надежностью 0,99 заключено истинное значение измеряемой величины.
. Найти границы, в которых с надежностью 0,99 заключено истинное значение измеряемой величины.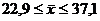 .
.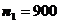 абитуриентов выдержали
абитуриентов выдержали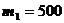 , на втором факультете из
, на втором факультете из 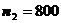 -
- 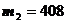 . На уровне значимости
. На уровне значимости 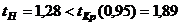 ).
).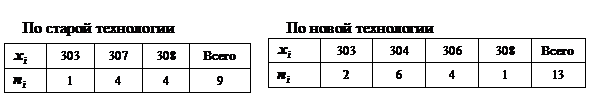
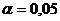 , выяснить, дает ли новая технология экономию в расходе сырья.
, выяснить, дает ли новая технология экономию в расходе сырья.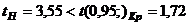 ).
).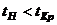 )
)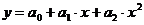 ).
).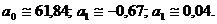
 ).
).