
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функции одного случайного аргумента. Законы распределения. Числовые характеристикиСлучайную величину Y называют функцией случайного аргумента X и записывают Если X - дискретная случайная величина и функциональная зависимость
Если же зависимость Если X - непрерывная случайная величина, заданная дифференциальной функцией
где х= В случае немонотонной зависимости
При известном законе распределения функции случайного аргумента  для дискретныхХ для непрерывныхХ
Однако Пример 7.1. Дискретная случайная величина Х задана законом распределения
Найти закон распределения функции 4 Составляем таблицу:
Так как все полученные значения уi различны и расположены в возрастающем порядке, эта таблица выражает закон распределения функции Пример 7.2. Дискретная случайная величина Х задана законом распределения
Найти закон распределения функции 4 Составляем таблицу:
Здесь есть два одинаковых значения у=0, им следует отвести один столбец, соответствующие вероятности сложить и расположить столбцы в порядке возрастания уi . Закон распределения У имеет вид:
Пример 7.3. Случайная величина X задана плотностью распределения вероятностей 4 Поскольку функциональная зависимость
итак,
Пример 7.4. Случайная величина Х задана дифференциальной функцией 4 Функция
Производные обратных функций соответственно равны:
и Так как Х принимает значения в интервале
Контроль: Пример 7.5. Закон распределения случайной величины Х имеет вид:
Найти математическое ожидание и дисперсию случайной величины 4Воспользуемся формулами, не вычисляя предварительно закон распределения случайной величины У:
= Пример 7.6. Плотность распределения случайной величины Х задана выражением: 4Воспользуемся формулами для вычисления математического ожидания и дисперсии функции непрерывного случайного аргумента Х, не находя предварительно закона распределения случайной величины У:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 393. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , если каждому значению X поставлено в соответствие некоторое значение Y. Возникает вопрос о нахождении закона распределения и числовых характеристик У по известному закону распределения Х.
, если каждому значению X поставлено в соответствие некоторое значение Y. Возникает вопрос о нахождении закона распределения и числовых характеристик У по известному закону распределения Х. монотонна, то различным значениям X будут соответствовать различные значения Y, причем вероятности соответствующих значений будут одинаковы. Т.е. если xi - возможные значения X, а
монотонна, то различным значениям X будут соответствовать различные значения Y, причем вероятности соответствующих значений будут одинаковы. Т.е. если xi - возможные значения X, а 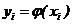 - полученные значения Y, то
- полученные значения Y, то  и закон распределения У имеет вид:
и закон распределения У имеет вид: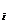 =j (х
=j (х  = j ( х
= j ( х  = j (х
= j (х  =j (х
=j (х  немонотонна, то различным значениям X могут соответствовать одинаковые значения Y. В таких случаях для отыскания вероятностей возможных значений Y следует сложить вероятности тех значений X, при которых Y принимает одинаковые значения и расположить все значения
немонотонна, то различным значениям X могут соответствовать одинаковые значения Y. В таких случаях для отыскания вероятностей возможных значений Y следует сложить вероятности тех значений X, при которых Y принимает одинаковые значения и расположить все значения 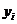 в порядке возрастания.
в порядке возрастания.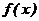 и функциональная зависимость
и функциональная зависимость  строго монотонна, то дифференциальная функция
строго монотонна, то дифференциальная функция 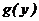 определяется равенством
определяется равенством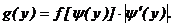 (7.1)
(7.1)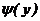 - обратная функция для функции
- обратная функция для функции 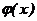 сохраняет монотонность, найти в соответствии с формулой (7.1)
сохраняет монотонность, найти в соответствии с формулой (7.1) 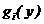 на каждом из этих интервалов и представить
на каждом из этих интервалов и представить  .
. ;
;  ;
; ;
;  ;
; и
и  можно получить, не определяя предварительно закон распределения функции
можно получить, не определяя предварительно закон распределения функции  . Рассмотрим примеры.
. Рассмотрим примеры. .
.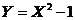 .
. . Найти дифференциальную функцию случайной величины
. Найти дифференциальную функцию случайной величины 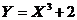 .
. монотонна на всей числовой оси, пользуемся готовой формулой
монотонна на всей числовой оси, пользуемся готовой формулой  , где
, где 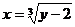 ;
;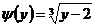 ,
,  ,
, 3
3 . Найти дифференциальную функцию распределения
. Найти дифференциальную функцию распределения  случайной величины
случайной величины  .
. на интервале
на интервале  не является монотонной. Разобьем этот интервал на две части
не является монотонной. Разобьем этот интервал на две части 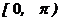 и
и  , в каждой из которых функция сохраняет монотонность. В интервале
, в каждой из которых функция сохраняет монотонность. В интервале  , обратная функция есть
, обратная функция есть  , в интервале
, в интервале  . Найдем
. Найдем 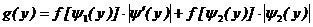 .
. ,
,  ,
,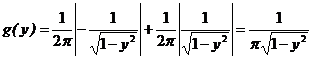 .
.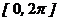 , то
, то  . Таким образом,
. Таким образом, .
. . 3
. 3 .
.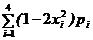 =
= ;
;
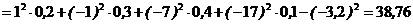 . 3
. 3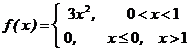 . Определить математическое ожидание и дисперсию случайной величины
. Определить математическое ожидание и дисперсию случайной величины  .
. ;
; 3
3