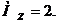Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Законы распределения функций двух случайных аргументов. Числовые характеристикиПусть случайная величина Z является функцией двух случайных величин, образующих систему (Х, У), т.е.
величина z содержится в этом выражении неявно в пределах интегрирования. Плотность распределения Z можно найти, дифференцируя G(z)по z:
При известном законе распределения случайной величины Z ее числовые характеристики можно вычислить по обычным правилам, но можно их определить и не прибегая к нахождению закона распределения Z. Для дискретных Х и Y:
Для непрерывных Х и Y:
4 Графиком функции Функция распределения
Дифференцируя по z, получим:
Пример 7.8.Система (Х,У) задана законом распределения
Найти закон распределения случайной величины Z =Х+У. 4 Находим значения xi+yj: -1, 0, 1, 2, 0, 1,2 , 3, 1, 2, 3, 4. Объединяя одинаковые и располагая их в порядке возрастания, получим возможные значения Z : –1, 0, 1, 2, 3, 4. Вычисляем соответствующие вероятности:
Искомый закон распределения Z имеет вид: Контроль: 0,01+0,1+0,34+0,29+0,17+0,09=1. 3
 Пример 7.9.Система (Х,У) задана плотностью распределения 4 Воспользуемся формулами (7.5) Получим: =
Пример 7.10. Система (Х, У) задана законом распределения
Вычислить математическое ожидание и дисперсию случайной величины 4 Не определяя закон распределения случайной величины Z, воспользуемся формулами
=
Теоремы о числовых характеристиках и их применение Процесс вычисления числовых характеристик функций случайных аргументов значительно упрощается, если использовать теоремі о свойствах числовых характеристик, особенно в тех случаях, когда функции – линейны. Теоремы о математических ожиданиях. 1. 2. 3. 4. 5. Если случайные величины Теоремы о дисперсиях 1. 2. 3. 4. Пример 7.11. Случайная величина Х – число автомобилей, реализуемых в течение одного дня автомобильным салоном, задана законом распределения
Номинальная стоимость одного автомобиля 3тыс. усл. ед. и за каждый день салон имеет 0,2 тыс. усл. ед. прибыли за счет дополнительных услуг. Указать среднюю выручку, получаемую салоном ежедневно и ее разброс. 4 Ежедневная выручка автомобильного салона есть случайная величина
На основании теорем о числовых характеристиках будем иметь:
Пример 7.12. Случайная величина Х задана плотностью распределения вероятностей 4 Функция Пример 7.13.Случайные величины Х и У, характеризующие соответственно расширение ассортимента выпускаемой продукции и изменение ее качества, заданы своими числовыми характеристиками 4 Согласно теоремам о числовых характеристиках, будем иметь:
Пример 7.14. Плотности распределения вероятностей независимых случайных величин Х и У заданы формулами:
Определить математическое ожидание и дисперсию случайной величины 4 Случайная величина Х распределена равномерно в интервале
Задачи 7.1. Случайная величина Х задана законом распределения
Составить закон распределения случайной величины У=X Ответ:
Система (Х,У) задана законом распределения:
Найти закон распределения и числовые характеристики случайной величины
в) г)
7.2. Случайная величина Х задана плотностью вероятности Ответ: М=1. 7.3. Дискретная случайная величина Х задана законом распределения:
Ответ: Р(Y≤4)=0,4
7.4. В партии из 10 деталей содержится 4 нестандартных. Наугад отобраны 2 детали. Записать законы распределения случайных величин Х={число стандартных деталей среди отобранных} и Ответ:
, Случайная величина Х задана плотностью распределения: Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величины Ответ: 7.5. Случайная величина Х задана функцией распределения Ответ: 7.6. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Y=sinX, если случайная величина Х задана законом распределения:
Ответ: 7.7. Партия из 10 деталей содержит 8 стандартных. Наугад отобраны 2 детали. Составить законы распределения случайной величины Х={число стандартных деталей среди двух отобранных} и случайной величины Ответ:
Р(Y>4)=28/45.
7.8. Найти математическое ожидание случайной величины Y=eX, если случайная величина Х задана функцией распределения:
Ответ: М= 0,5( е 7.9. Дискретная случайная величина Х имеет возможные значения Х={-2,0,3}. Известно, что математическое ожидание величины Х равно 1.0; а дисперсия равна 1.4. Найти законы распределения случайной величины Х и случайной величины Y=X2. Ответ:
7.12. Дана плотность вероятности случайной величины: Ответ: а= 2; 7.13. Случайная величина Х задана функцией распределения Рэлея: Ответ: 7.14. Партия из 5 изделий проверяется на стандартность. Вероятность того, что изделие стандартно, равна 0.8. Определить математическое ожидание и дисперсию случайной величины Х={число стандартных изделий в партии}, а также математическое ожидание и дисперсию случайной величины Y=3X-1. Ответ: 7.15. Плотность распределения случайной величины Х: Ответ: а = 1/p; 7.16. Дискретная случайная величина Х задана законом распределения:
Вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Ответ: 7.17. Задана функция распределения случайной величины Х: Ответ: Р = 0,00195. 7.18. Случайная величина Х может принимать значения: Х={-1,0,1}. Известно, что математическое ожидание величины Х равно 0, а дисперсия равна 0.08. Составить законы распределения случайных величин Х и Y=X2. Ответ:
7.19. Случайная величина Х задана рядом распределения:
Найти функцию распределения F(y), построить ее график и вычислить вероятность события (Y Ответ:
. Р(У<3)=Р(У£3)=1.
7.20. Случайная величина Х имеет плотность вероятностей: Найти математическое ожидание и дисперсию случайной величины Y=eX. Ответ: Му=0,5е
7.21. Производится два выстрела с вероятностями попадания в цель при каждом выстреле соответственно 0.6. Составить законы распределений случайной величины Х={ число попаданий при двух выстрелах} и величины Y=2X+2. Ответ:
7.22. Случайная величина Х имеет плотность распределения вероятностей: Ответ: 7.23. Определить математическое ожидание и дисперсию случайной величины Z=4X+Y, если X и Y - независимые нормально распределенные случайные величины с плотностями распределений: Ответ: 7.24. Определить математическое ожидание случайной величины Z= XY+X, если X и Y - случайные величины с известными mx=2, my= ‑2 и Kxy= ‑3. Ответ: 7.25. Заданы две независимые случайные величины X и Y. Величина Х распределена по показательному закону с параметром Ответ: 7.26. Определить математическое ожидание и дисперсию случайной величины Z=4X-2Y, если X и Y - случайные величины с известными характеристиками mx=2, my=-1, Dx=4, Dy=2, Kxy=2. Ответ: 7.27. Случайная величина Х распределена равномерно в интервале Ответ: 7.28. Случайная величина Х равномерно распределена в интервале (0,3). Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Ответ: 7.29. Заданы две независимые случайные величины X и Y. Величина Х распределена равномерно на интервале (‑3, 1), величина Y распределена по показательному закону с параметром Ответ: 7.30. Определить математическое ожидание и дисперсию случайной величины Z=3X+4Y, если X и Y - случайные величины с известными характеристиками mx=‑2, my=1, Dx=3, Dy=1, Kxy=4. Ответ: 7.31. Определить математическое ожидание и дисперсию случайной величины Z= ‑X+3Y, если X и Y - случайные величины с известными характеристиками mx= ‑1, my=2, Dx=1, Dy=3, Kxy= ‑2 Ответ: 7.32. Заданы две независимые случайные величины X и Y. Величина Х распределена нормально с плотностью вероятности Ответ:
ГЛАВА 8. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Установление статистических закономерностей, присущих массовым случайным явлениям, основано на изучении статистических данных – сведений о том, какие значения принял в результате наблюдений интересующий нас признак. В математической статистике изучаются две основные задачи: - указать способы сбора и группировки статистических сведений (данных), полученных в результате наблюдений или поставленных экспериментов (здесь не рассматриваются); - разработать методы анализа статистических данных в зависимости от поставленных целей исследования. С математической статистикой тесно связаны такие науки как планирование эксперимента, последовательный анализ данных, регрессионный анализ, эконометрика и ряд других. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 409. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
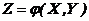 . Для непрерывной системы (Х,У) с известной плотностью распределения вероятностей
. Для непрерывной системы (Х,У) с известной плотностью распределения вероятностей 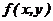 , закон распределения Z следует определять, начиная с построения интегральной функции
, закон распределения Z следует определять, начиная с построения интегральной функции  :
: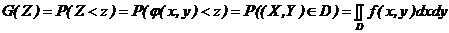 , (7.2)
, (7.2)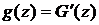 . (7.3)
. (7.3)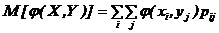 ;
; 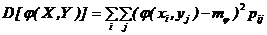 . (7.4)
. (7.4)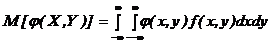 ;
; 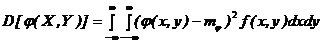 . (7.5)
. (7.5)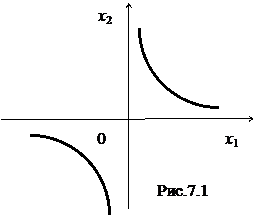 Пример 7.7. Система (Х1,Х2) задана плотностью распределения
Пример 7.7. Система (Х1,Х2) задана плотностью распределения 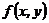 ; величина Z есть произведение случайных величин
; величина Z есть произведение случайных величин 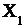 и
и 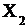 ;
; 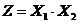 . Найти плотность распределения величины Z.
. Найти плотность распределения величины Z.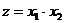 является гипербола
является гипербола 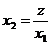 . (Рис. 7.1).
. (Рис. 7.1).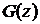 имеет вид:
имеет вид: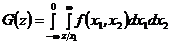 +
+ 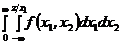 .
.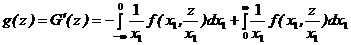 . 3
. 3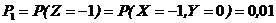 ;
;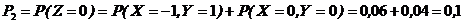 ; и т.д.
; и т.д.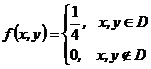 , где
, где 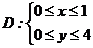 . Вычислить числовые характеристики
. Вычислить числовые характеристики 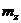 и
и 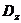 случайной величины
случайной величины 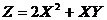 .
.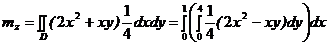 =
=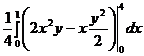 =
= 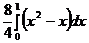 =
= 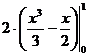 =
= 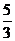 ,
,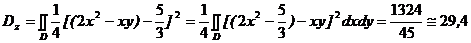 . 3
. 3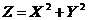 .
.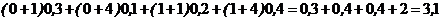
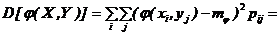
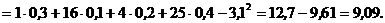 3
3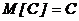
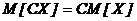

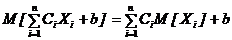
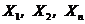 независимы, то
независимы, то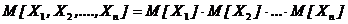
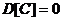
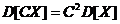
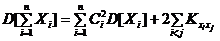 , где
, где 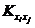 - корреляционный момент пары случайных величин
- корреляционный момент пары случайных величин 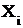 и
и 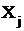 .
.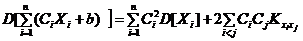
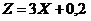 , и для решения задачи требуется определить
, и для решения задачи требуется определить 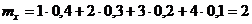 - в среднем продается 2 автомобиля в день;
- в среднем продается 2 автомобиля в день; 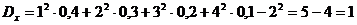 ,
,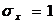 -разброс продажи составляет 1 автомобиль в день.
-разброс продажи составляет 1 автомобиль в день.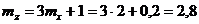 тыс.усл.ден.ед. – средняя ежедневная выручка;
тыс.усл.ден.ед. – средняя ежедневная выручка; 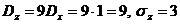 тыс.усл.ден.ед. – разброс от средней выручки. 3
тыс.усл.ден.ед. – разброс от средней выручки. 3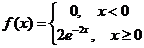 . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины 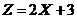 .
.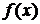 представляет собой плотность показательного закона распределения, а это значит, что
представляет собой плотность показательного закона распределения, а это значит, что 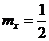 и
и 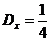 . Тогда согласно теоремам о числовых характеристиках
. Тогда согласно теоремам о числовых характеристиках 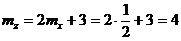 и
и 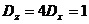 . 3
. 3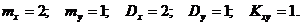 Вычислить числовые характеристики
Вычислить числовые характеристики 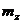 и
и 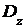 случайной величины
случайной величины 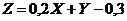 , характеризующей колебания прибыли предприятия.
, характеризующей колебания прибыли предприятия.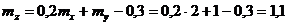 ;
; 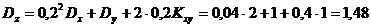 . 3
. 3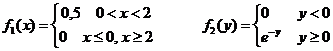 .
.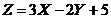 .
.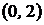 , это значит, что
, это значит, что 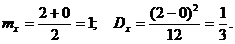 Случайная величина У подчинена показательному закону распределения, следовательно
Случайная величина У подчинена показательному закону распределения, следовательно 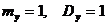 . Так как Х и У независимы, то
. Так как Х и У независимы, то 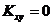 и согласно теоремам о числовых характеристиках, получим
и согласно теоремам о числовых характеристиках, получим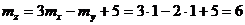 ;
; 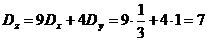 . 3
. 3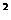 вычислить
вычислить 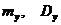
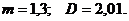 s =1,45
s =1,45
 : а) Z=X+Y; б) Z=XY; в) Z=2X-3Y; г)
: а) Z=X+Y; б) Z=XY; в) Z=2X-3Y; г) 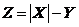 .
. Ответ: а) б)
Ответ: а) б)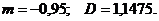 ; s =1,07.
; s =1,07. 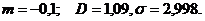 ;
; 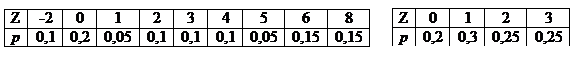
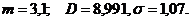
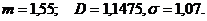
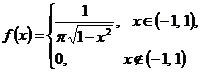 . Найти математическое ожидание случайной величины
. Найти математическое ожидание случайной величины 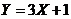 .
.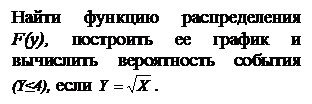
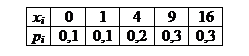

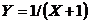 .
.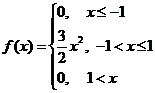 .
.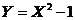 .
.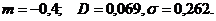
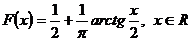 .Найти плотность распределения g(y) случайной величины
.Найти плотность распределения g(y) случайной величины 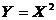 .
. 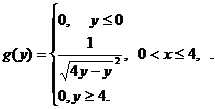
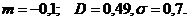
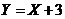 . Определить вероятность того, что Y>4.
. Определить вероятность того, что Y>4. 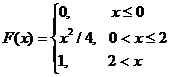 .
.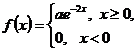 . Найти коэффициент а и плотность вероятности случайной величиной Y= eX .
. Найти коэффициент а и плотность вероятности случайной величиной Y= eX .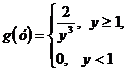
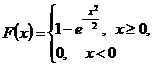 .Найти плотность распределения
.Найти плотность распределения  случайной величины Y=eX.
случайной величины Y=eX. 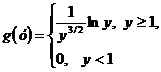
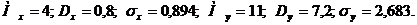
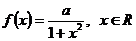 . Найти коэффициент а и плотность вероятности величины Y=X2.
. Найти коэффициент а и плотность вероятности величины Y=X2. 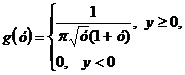
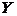 = cos X.
= cos X.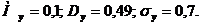
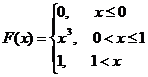 . Определить вероятность того, что 0.2≤Y≤0.5, если Y=
. Определить вероятность того, что 0.2≤Y≤0.5, если Y= 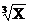 .
.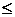 3), если Y=X2.
3), если Y=X2.
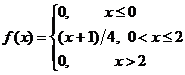 .
. –1)/16.
–1)/16.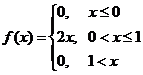 . Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величины Y=
. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величины Y=  .
. 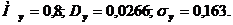
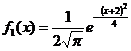 ,
, 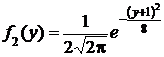 .
.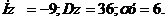
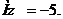
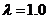 ; величина Y распределена по тому же закону с параметром
; величина Y распределена по тому же закону с параметром  . Определить математическое ожидание и дисперсию случайной величины Z=‑3X+2Y.
. Определить математическое ожидание и дисперсию случайной величины Z=‑3X+2Y.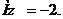
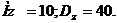
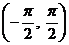 . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.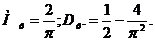
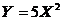 .
. 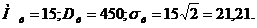
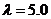 . Определить математическое ожидание случайной величины Z= 5XY-3X.
. Определить математическое ожидание случайной величины Z= 5XY-3X.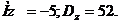
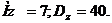
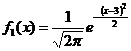 , величина Y распределена равномерно на интервале (‑5, 1). Определить математическое ожидание случайной величины Z= -2XY-10.
, величина Y распределена равномерно на интервале (‑5, 1). Определить математическое ожидание случайной величины Z= -2XY-10.