
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Генеральная и выборочная совокупность.Вся совокупность объектов, изучаемая относительно некоторого количественного признака Х (случайной величины) называется генеральной совокупностью. Количество объектов в ней может быть и не известно. Любое количество объектов, каким-либо образом отобранных из генеральной совокупности называется выборочной совокупностью или просто выборкой. Полное количество членов в любой из совокупностей называется ее объемом. Вариационный ряд. Представление и первоначальная обработка Различные значения признака Х, обозначаемые
а ширину интервала -
Пример 8,1. Изучается выработка на одного рабочего предприятия в текущем году, взятая в процентах по отношению к прошлому году. Пусть из генеральной совокупности (общего числа сотрудников) сделана выборка объемом n=100. Получены следующие данные:
X={101, 98, 110, 111, 100, 97, 102, 89, 94, 101, 113, 95, 90, 92, 89, 102, 100, 93, 116, 96, 106, 105, 98, 101, 112, 97, 101, 104, 97, 100, 100,112, 103, 109, 94, 94, 94, 101, 96, 100, 97, 102, 89, 100,112, 102, 100, 94, 104, 99, 110, 111, 101, 100, 101, 103, 99, 94, 101, 98, 111, 111, 102, 101, 111, 96, 103, 104, 97, 99, 100, 100,112, 103, 109, 94, 113, 96, 106, 105, 98, 101, 111, 97, 101, 106, 97, 100, 107,112, 113, 96, 106, 105, 98, 101, 112, 97, 101, 104,}.  Требуется построить статистические ряды. 4Расположим признак в порядке возрастания вариант. X={89, 89, 89, 90, 92, 93, 94, 94, 94,94, 94, 94, 94, 95, 96, 96, 96, 96, 96, 97, 97, 97, 97, 97, 97, 97, 97, 98, 98, 98, 98, 98, 99, 99, 99, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 101, 101, 101, 101, 101, 101, 101 101, 101, 101, 101, 101, 101, 102, 102, 102, 102, 102, 103, 103, 103, 103, 104, 104, 104, 104, 105, 105, 105, 106, 106, 106, 106, 107, 109, 109, 110, 110, 111, 111, 111, 111, 111, 111, 112, 112, 112, 112, 112, 112, 113, 113, 113, 116}.
Подсчитаем количество повторяющихся вариант и построим простой статистический ряд в виде таблицы 1:
Таблица 1.
Здесь Учитывая, что в большинстве случаев каждое значение варианты встречается редко, 1–3 раза, перейдем к вариационному интервальному ряду.
За начало первого интервала рекомендуется брать величину Таблица 2.
Числа
Графические характеристики выборки Такими характеристиками служат эмпирическая функция распределения, полигон частот (относительных частот) и гистограмма. Эмпирической функцией распределения
Полигон частот – ломаная, концы отрезков которой имеют координаты Гистограмма служит для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру, состоящую из прямоугольников с основаниями, равными интервалам значений признака
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 402. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
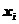 называются вариантами. Выборка, упорядоченная по возрастанию
называются вариантами. Выборка, упорядоченная по возрастанию  ,
, , где
, где  - разность между наибольшей и наименьшей вариантами, а n – объем выборки.
- разность между наибольшей и наименьшей вариантами, а n – объем выборки.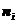
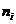 - количество появлений значения признака (варианты)
- количество появлений значения признака (варианты) 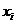 в выборке. Очевидно, что
в выборке. Очевидно, что  .
.
 ; примем:
; примем:  (%).
(%). В данном случае
В данном случае  . Сгруппированный вариационный ряд представляется в виде таблицы 2:
. Сгруппированный вариационный ряд представляется в виде таблицы 2:

 – частностями или относительными частотами.
– частностями или относительными частотами. называется относительная частота того, что признак (случайная величина Х) примет значение, меньше заданного х,т.е.
называется относительная частота того, что признак (случайная величина Х) примет значение, меньше заданного х,т.е.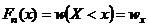
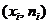 или
или  - для полигона относительных частот. Полигон частот используется для графического представления простого статистического ряда.
- для полигона относительных частот. Полигон частот используется для графического представления простого статистического ряда.


