
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей. Критерий Фишера-Снедекора.Пусть имеются две нормально распределенных совокупности, дисперсии которых Конкурирующая гипотеза Статистика для проверки:
Критическое значение критерия Фишера-Снедекора определяется по таблицам: Пример 8,3. Проверяется точность изготовления детали на двух станках x и y. Извлечены выборки объемами 4
8.5.3. Сравнение выборочной средней с гипотетической генеральной средней нормально распределенной совокупности а) дисперсия генеральной совокупности известна. Нулевая гипотеза Конкурирующая гипотеза Статистика для проверки: Критическое значение критерия определяется по таблицам интеграла Лапласа: Если
Нулевая гипотеза Конкурирующая гипотеза Критическое значение критерия определяется по таблицам интеграла Лапласа: Если
Нулевая гипотеза Конкурирующая гипотеза Критическое значение критерия определяется по таблицам интеграла Лапласа: Если
б) дисперсия генеральной совокупности неизвестна. Нулевая гипотеза Конкурирующая гипотеза Статистика для проверки:  Критическое значение критерия определяется по таблицам двусторонних критических точек распределения Стьюдента Если
Нулевая гипотеза Конкурирующая гипотеза Критическое значение критерия определяется по таблицам право-сторонних критических точек распределения Стьюдента Если,
Нулевая гипотеза Конкурирующая гипотеза Критическое значение критерия определяется по таблицам право-сторонних критических точек распределения Стьюдента Если, Для примера 8.1 проверим выполнение гипотезы 3
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 361. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и 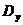 . Проверяется гипотеза:
. Проверяется гипотеза: 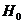 :
:  .
.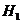 :
:  .
. ;
; , где
, где 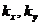 - числа степеней свободы дисперсий. Если
- числа степеней свободы дисперсий. Если 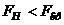 , то нет основания отвергнуть нулевую дисперсию.
, то нет основания отвергнуть нулевую дисперсию.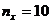 и
и 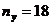 изделий соответственно. При этом рассчитаны исправленные выборочные дисперсии
изделий соответственно. При этом рассчитаны исправленные выборочные дисперсии  и
и 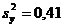 . На уровне значимости
. На уровне значимости  проверить нулевую гипотезу
проверить нулевую гипотезу 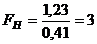 .
. 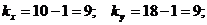 По таблицам находим:
По таблицам находим:  . Так как
. Так как  , то нулевая гипотеза отвергается, т.е. станки не обеспечивают одинаковую точность. 3
, то нулевая гипотеза отвергается, т.е. станки не обеспечивают одинаковую точность. 3 .
. ;
;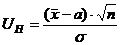 ;
; .
. , то нулевая гипотеза не отвергается.
, то нулевая гипотеза не отвергается. ;
; .
. ;
; .
. , то нулевая гипотеза не отвергается.
, то нулевая гипотеза не отвергается. , где
, где  имеет распределение Стьюдента с
имеет распределение Стьюдента с 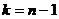 степенями свободы дисперсии.
степенями свободы дисперсии. .
. , то нулевая гипотеза не отвергается.
, то нулевая гипотеза не отвергается. .
.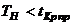 ,то нулевая гипотеза не отвергается.
,то нулевая гипотеза не отвергается. .
. ,то нулевая гипотеза не отвергается.
,то нулевая гипотеза не отвергается. при конкурирующей гипотезе
при конкурирующей гипотезе 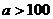 и уровне значимости
и уровне значимости 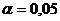

 .
.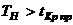 , поэтому нулевую гипотезу следует отвергнуть в пользу конкурирующей и признать, что выработка возросла. 4
, поэтому нулевую гипотезу следует отвергнуть в пользу конкурирующей и признать, что выработка возросла. 4