
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Точечные характеристики выборки (оценки параметров)Вариационный ряд является статистическим аналогом (реализации) распределения признака (случайной величины Х). В этом смысле полигон (гистограмма) аналогичен кривой распределения - дифференциальной функции распределения случайной величины Х. Однако построение их достаточно громоздко. В то же время, на практике часто оказывается достаточным знание лишь числовых характеристик случайной величины (признака Х)- математического ожидания, дисперсии и т.д. Но числовые характеристики Х неизвестны и информация о них может быть получена только на основе изучения имеющихся опытных данных – выборки. В математической статистике принято говорить, что некоторые сводные характеристики выборки служат для оценивания (являются оценкой) числовых характеристик генеральной совокупности. Эти характеристики носят название точечных оценок выборки. Расчет их – следующий этап обработки опытных данных. К точечным оценкам предъявляются требования несмещенности, состоятельности и эффективности. Оценка
Оценка
Эффективной называется та оценка, которая имеет наименьшую дисперсию среди других возможных оценок. Рассмотрим эти оценки. Выборочная средняя – (аналог математического ожидания с.в.) -средняя арифметическая значений вариант, рассчитанная по значениям вариационного ряда:
 Выборочная дисперсия – (аналог дисперсии с.в.) - средняя арифметическая квадратов отклонения вариант от выборочной средней; служит характеристикой рассеяния вариант относительно выборочной средней:
Выборочная дисперсия не удовлетворяет свойству несмещенности, поэтому вводится также исправленная выборочная дисперсия:
Желательно в качестве меры рассеяния иметь характеристику, выраженную в тех же единицах, что и варианты. Поэтому вводится среднее выборочное квадратическое отклонение:
Рассматривается также безразмерная характеристика – коэффициент вариации, который служит для оценки однородности опытных данных: Мода Медиана Для дискретного ряда из нечетного числа членов медиана равна серединной варианте, для ряда из четного числа членов – полусумме двух серединных вариант. Рассчитаем эти оценки для примера 1. 4Выборочная средняя: а) Для простого вариационного ряда (таблица 1):
б) Для интервального вариационного ряда (таблица 2):
Выборочная дисперсия: а) Для простого вариационного ряда:
б) Для интервального вариационного ряда;
Исправленная выборочная дисперсия и среднее выборочное квадратическое отклонение: а) Для простого вариационного ряда:
Коэффициент вариации: а) Для простого вариационного ряда: б) Для интервального вариационного ряда; Мода и медиана: а) Для простого вариационного ряда:
б) Для интервального вариационного ряда;
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 335. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
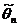 параметра
параметра  генеральной совокупности называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.
генеральной совокупности называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е. .
. называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
называется состоятельной, если она сходится по вероятности к оцениваемому параметру: .
. (8.3.1),
(8.3.1),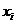 - варианты простого статистического ряда или середины интервалов вариационного;
- варианты простого статистического ряда или середины интервалов вариационного; 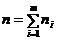 .
. (8.3.2.).
(8.3.2.).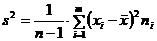 (8.3.3.).
(8.3.3.). (8.3.4.).
(8.3.4.). % (8.3.5.).
% (8.3.5.). – варианта, которой соответствует наибольшая частота;
– варианта, которой соответствует наибольшая частота;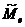 – значение признака, приходящееся на середину вариационного ряда (количество вариант меньших
– значение признака, приходящееся на середину вариационного ряда (количество вариант меньших 



 б) Для интервального вариационного ряда;
б) Для интервального вариационного ряда;


