
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Числовые характеристики системы случайных величинЗакон распределения полностью характеризует систему случайных величин, но использовать его на практике не всегда удобно в силу сложности. Зачастую бывает достаточно знать числовые характеристики составляющих систему случайных величин, к которым относятся: математические ожидания M[X], M[Y], дисперсии D[X], D[Y] и среднеквадратические отклонения Для дискретных систем случайных величин
Для непрерывных систем случайных величин
Дисперсии составляющих можно вычислять и по укороченным формулам:
Важную роль в теории двумерных случайных величин играет корреляционный момент (ковариация)
Корреляционный момент вычисляется по следующим формулам. Для дискретных систем случайных величин
Для непрерывных систем случайных величин
Наряду с корреляционным моментом используется безразмерная характеристика корреляционной связи - коэффициент корреляции
Для любых систем случайных величин Условным законом распределения случайной величины, входящей в систему, называется закон ее распределения, вычисленный при условии, что другая случайная величина приняла определенное значение. Для систем непрерывных случайных величин условные законы выражаются условными плотностями распределения составляющих:
 |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 352. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Они вычисляются по следующим формулам.
. Они вычисляются по следующим формулам.
 ;
; 

 ;
; 
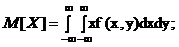
 ;
; 
 ;
;

 , характеризующий линейную связьмежду составляющими системы:
, характеризующий линейную связьмежду составляющими системы: . (6.7)
. (6.7)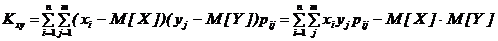 .
. =
= 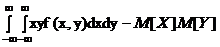
 (6.8)
(6.8) Случайные величины Х и Y называются некоррелированными, если
Случайные величины Х и Y называются некоррелированными, если  .Независимые величинывсегда некоррелированы.
.Независимые величинывсегда некоррелированы.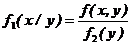 , при этом
, при этом  , (6.9)
, (6.9) , при этом
, при этом 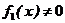 .
.