
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Глава 6. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Закони распределения систем случайных величин. Несколько случайных величин, рассматриваемых совместно, образуют систему случайных величин, обозначаемую (X,Y), (X,Y,Z), ... . В дальнейшем рассматриваются системы двух случайных величин (случайные векторы) (Х,Y), где Х, Y – составляющие системы, могут быть дискретными или непрерывными. Охарактеризовать систему (Х,Y) можно законом ее распределения. Законом распределения (X,Y)называется соотношение, устанавливающее связь между областями ее значений и соответствующими вероятностями. Закон распределения двумерной дискретной случайной величины задается в виде таблицы 1: Таблица 1
где
и геометрически представляет собой вероятность попадания случайной точки с координатами (Х,У) в бесконечный прямоугольник с вершиной в точке М(х;у), лежащий левее и ниже ее.
Для систем дискретных случайных величин интегральная функция распределения:
Для систем непрерывных случайных величин интегральная функция распределения:
где
Свойства интегральной функции распределения: 1) 2) 3) 4)  Свойства дифференциальной функции распределения (плотности вероятности): 1) 2) 3) 4) вероятность попадания случайной точки (Х,Y) в область D :
Случайные величины Х и Y являются независимыми, если Одномерные плотности вероятностей составляющих системы:
Для системы независимых случайных величин Х и Yдвумерная плотность вероятности равна произведению плотностей распределения вероятностей составляющих:
В случае системы дискретных случайных величин можно построить безусловные законы распределения составляющих в виде таблиц 2 и 3. Таблица 2
Таблица 3
Пример 6.1.Передаются два сообщения, каждое из которых может быть независимо друг от друга либо искажено, либо не искажено. Вероятность события А {сообщение искажено} для первого сообщения равна 0,2, для второго - 0,3. Рассматривается система двух случайных величин (Х,У), определяемых так: Х=0, если первое сообщение не искажено, Р(X=0)=0,8; X=1, если первое сообщение искажено, Р(X=1)=0,2; Y=0, если второе сообщение не искажено, Р(Y=0)=0,7; Y=1, если второе сообщение искажено, Р(Y=1)=0,3; Найти закон совместного распределения системы (Х,Y). 4 Так как случайные величины, входящие в систему, дискретны, то закон распределения должен быть выражен в виде таблицы 1. Вероятности
Закон распределения системы (Х,У) имеет вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 350. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |










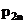




 - вероятность события, заключающегося в совместном выполнении равенств
- вероятность события, заключающегося в совместном выполнении равенств  причем
причем  .
. Интегральная функция распределения вероятностей системы случайных величин (Х,У) определяется:
Интегральная функция распределения вероятностей системы случайных величин (Х,У) определяется: (6.1)
(6.1) . (6.2)
. (6.2)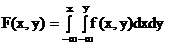 , (6.3)
, (6.3) ‑ плотность распределения вероятностей или дифференциальная функция распределения системы случайных величин (Х,У):
‑ плотность распределения вероятностей или дифференциальная функция распределения системы случайных величин (Х,У): (6.4)
(6.4) .
. .
. .
. .
.
 (условие нормировки);
(условие нормировки); ;
;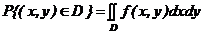 . (6.5).
. (6.5). , где F1(x), F2(y) – безусловные интегральные функции распределения составляющих системы.
, где F1(x), F2(y) – безусловные интегральные функции распределения составляющих системы. (6.5).
(6.5). (6.6)
(6.6)
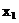









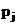


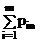
 определятся следующим образом.
определятся следующим образом. ;
;  ;
;  ;
;  .
. \
\ 