
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нормальное распределение СВ.5.25. Текущая цена акции моделируется нормальным законом распределения с математ. ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед. Найти: 1 вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. 2. С помощью правила Ответ: 1. а) 0,4332; б) 0,0228; в) 0,6246; 2. 5.26. Цена акции распределена нормально. В течение последнего года 20% рабочих дней она была ниже 88 ден. ед., а 75% - выше 90 ден. ед. Найти: а) математическое ожидание и среднее квадратическое отклонение цены ценной бумаги; б) вероятность того, что в день покупки цена будет заключена в пределах от 83 до 96 ден. ед.; в) с надежностью 0,95 определить максимальное отклонение цены от среднего (прогнозного) значения по абсолютной величине. Ответ: а) М(х) = 98; σ = 12; б) 0,33; в) 5.27. По многолетним наблюдениям за балансовой прибылью фирмы установлено, что эта прибыль меняется в пределах от 10000 до 40000грив. в месяц. Считая, что она распределена нормально, определить параметры этого распределения и найти вероятность того, что балансовая прибыль в следующем месяце составит 24000-28000 гривен. Указание. Из неравенства Ответ: 5.28. Система, "следящая" за процессом ценообразования, содержит систематические и случайные ошибки. Систематическая ошибка равна 0,5 цента в сторону занижения. Случайные ошибки подчиняются нормальному закону распределения со средним квадратичным отклонением s=1цент. Найти а) вероятность фиксации цены по абсолютной величине 1,5 цента; б) вероятность того, что фиксированная цена не превзойдет истинной.  Ответ: 5.29. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратичным отклонением s=20г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10г. Ответ: 5.30. Фирма изготавливает железобетонные изделия, используя в качестве основного сырья цемент. В связи с неопределенностью спроса на эти изделия потребность в цементе меняется из месяца в месяц, причем в среднем она составляет 2500 т/мес., а ее разброс характеризуется среднеквадратичным отклонением 600 т/мес. Считая распределение потребности в цементе нормальным, определить вероятность того, что в следующем месяце она не выйдет за пределы 2200-2700 т. Ответ: 5.31. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со средним квадратичным отклонением s=5мм. и математическим ожиданием а=0. Сколько процентов годных деталей изготавливает автомат? Ответ: 5.32. Нормально распределенная СВ Х задана плотностью вероятности Ответ: 5.33. СВ Х распределена нормально с математическим ожиданием а=10 и средним квадратичным отклонением s=5. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадет величина Х в результате испытания. Ответ: Другие законы распределения 5.34. СВ Х задана функцией распределения Рэлея: Ответ: 5.35. Дана функция распределения Рэлея: Ответ: 5.36. Дана плотность вероятности СВ Х: Ответ: 5.37. Дана плотность вероятности СВ: Ответ: а = 0,25;
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 498. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
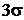 найти границы, в которых будет находиться текущая цена акции.
найти границы, в которых будет находиться текущая цена акции. .
.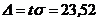 .
. , предварительно найти
, предварительно найти 
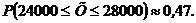
 .
.

 , т.е. автомат изготовил примерно 95%.
, т.е. автомат изготовил примерно 95%. . Найти моду и медиану.
. Найти моду и медиану.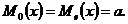
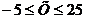 .
. Найти плотность распределения
Найти плотность распределения  величины Х.
величины Х.

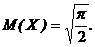
 . Найти коэффициент а и моду.
. Найти коэффициент а и моду.