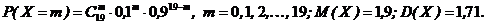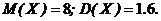Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Показательное распределениеНепрерывная СВ Х распределена по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей имеет вид: где l - параметр распределения. Кривая плотности распределения f(x)изображена на рис.5.3. Интегральная функция распределения равна ее график показан на рис 5.4.
Математическое ожидание, дисперсия и среднее квадратичное соответственно равны: M[X]=1/l; D[X]=1/l2; sх=1/l; (5.13) а вероятность попадания Х в заданный интервал значений
Пример 5.5.СВ Т—время безотказной работы телевизора - имеет показательное распределение. Определить вероятность того, что время безотказной работы телевизора будет не меньше 600 часов, если среднее время работы его 400 часов. 4 По условию задачи математическое ожидание СВ Т равно 400 часов. Искомая вероятность P(T ³ 600 )= 1- P(T<600 )= 1- F(600)=1-(1-e-600/400 )=e-1,5 » 0,2231. 3 Нормальное распределение СВ Х подчинена нормальному закону распределения,если ее плотность распределения вероятностей имеет вид:
где a ‑ математическое ожидание, Интегральная функция нормального распределения имеет вид
где Основные свойства функции Лапласа: 1) F(0) = 0; 2) 3) F(¥)=0,5 Таблица значений функции F(х) для  Вероятность попадания Х в заданный интервал значений
Вероятность того, что абсолютная величина отклонения В частности, при а=0, P(êХ ê<d) =2F(d/s). Если в равенстве 5.17. т.е. отклонение нормальной СВ от своего математического ожидания а на величину, равную
Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
График плотности вероятности нормального распределения (рис.5.5) называют нормальной кривой (кривой Гаусса). Пример 5.6. Ошибка измерения длины платформы станции метро подчинена нормальному закону. Математическое ожидание этой ошибки равно 5см, а среднее квадратичное отклонение равно 10см. Найти вероятность того, что измеряемое значение длины платформы будет отклоняться от истинного не более чем на 20см. 4Решение задачи сводится к определению вероятности попадания СВ Х (ошибка измерения) с математическим ожиданием а=5см и средним квадратичным отклонением s=10см в интервал значений (‑20, 20).По формуле вычисления вероятности попадания Х в заданный интервал имеем: P(‑20<Х<20) = Пример 5.7. Доказать, что параметр а нормальной плотности распределения СВ Х является математическим ожиданием Х. 4Доказательство. По определению:
(так как Задачи Биномиальный закон. 5.1. Вероятность выигрыша по облигации займа за все время его действия равна 0,1. Составить закон распределения числа выигравших облигаций среди приобретенных 19. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение. Ответ: 5.2. Партия из 10 изделий проверяется на стандартность. Вероятность того, что изделие стандартно, равна 0.8. Определить математическое ожидание и дисперсию СВ Х = {число стандартных изделий в партии}. Ответ: 5.3. В большой партии 20% нестандартных деталей. Из них наудачу отобраны 5 деталей. а) написать биномиальный закон распределения дискретной СВ Х - числа нестандартных деталей среди пяти отобранных; б) построить многоугольник распределения; в) найти математическое ожидание и среднее квадратичное отклонение.
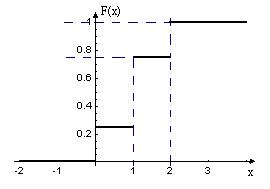
M(X) = 1; 5.4. Написать биномиальный закон распределения дискретной СВ Х ‑ числа появлений “герба” при двух бросках монеты. Построить функцию распределения.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 434. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
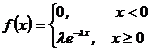 , (5.12)
, (5.12)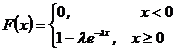 , (5.13)
, (5.13)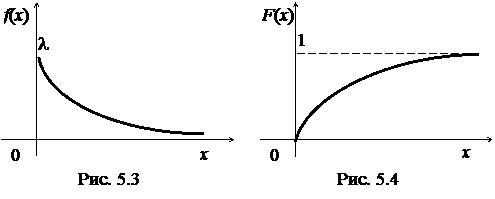
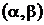 определяется следующим образом:
определяется следующим образом: 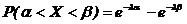 .
.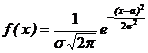 , (5.14)
, (5.14)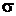 ‑ среднее квадратичное отклонениеХ.
‑ среднее квадратичное отклонениеХ.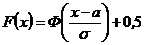 ; (5.15)
; (5.15)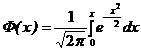 - функция Лапласа, или интеграл вероятностей.
- функция Лапласа, или интеграл вероятностей.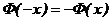 (нечетная функция);
(нечетная функция); 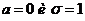 приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.
приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.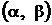 :
: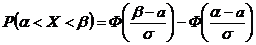 , (5.16)
, (5.16)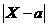 нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:
нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением: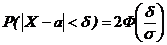 . (5.17)
. (5.17)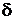 взять
взять 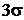 , получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле,
, получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле, 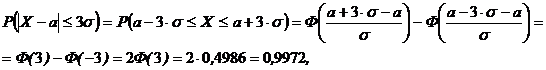
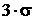 является событием практически достоверным.
является событием практически достоверным.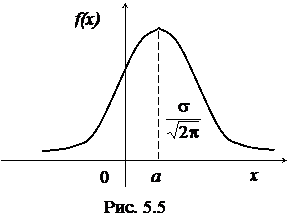 аs=0, еk=0, Mo=a, Me=a, где a=M[X].
аs=0, еk=0, Mo=a, Me=a, где a=M[X].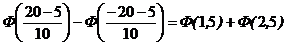 =
= 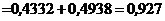 .3
.3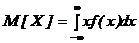 . Для нормального распределения получим:
. Для нормального распределения получим: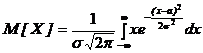 =
= 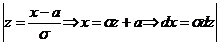 = =
= = 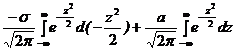 =
= 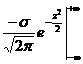 +
+  =a
=a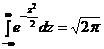 ). 3
). 3