
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Гипергеометрическое распределение5.5. В партии из 10 деталей имеется 8 стандартных. Наугад отобраны 2 детали. Составить закон распределения числа стандартных деталей среди отобранных. Определить вероятность того, что число стандартных деталей среди отобранных будет меньше двух.
; Р(Х<2) =
5.6. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения СВ Х ‑ числа стандартных деталей среди отобранных. Построить функцию распределения. Найти M[X], D[X], sx.
5.7. Партия из 20 деталей содержит 16 стандартных. Наугад отобраны 4 детали. Составить закон распределения СВ Х = {число стандартных деталей среди четырёх отобранных}. Определить вероятность того, что среди отобранных деталей число стандартных будет не меньше двух.
Р(2<Х<4) = 0.987.
5.8. В партии из 10 деталей содержится 4 нестандартных. Наугад отобраны 2 детали. Найти дисперсию и среднее квадратичное отклонение СВ Х={число стандартных деталей среди отобранных}. Ответ: 5.9. В партии из 10 деталей содержится 4 нестандартных. Наугад отобраны 3 детали. Записать закон распределения СВ Х={число стандартных деталей среди отобранных}. Определить вероятность того, что число нестандартных деталей среди отобранных будет не меньше двух.
p=1/3.
5.10.  Ответ: M(X) = 2.8; Распределение Пуассона 5.11. СВ Х представляет число бракованных деталей из возвратной выборки в 50 штук. Вероятность брака одной детали p=0,06. Найти математическое ожидание, дисперсию и средне квадратичное отклонение числа бракованных деталей в выборке. Ответ: 5.12. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут : а) ровно три; б) менее трех; в) более трех; г) хотя бы одно. Ответ:
5.13. Найти среднее число l - бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0,95. Предполагается, что число бракованных изделий распределено по закону Пуассона. Ответ: Равномерное распределение 5.14. Предполагая, что индекс цен на продовольственные товары равномерно распределен в пределах от 110 до 150%, найти вероятность того, что он не превысит 135%, а также вычислить характеристики его разброса. Ответ: 5.15. Коммерческая маржа Х посреднической фирмы равномерно распределена с параметрами Ответ: 5.16. Минутная стрелка электрических часов передвигается скачками поминутно. Вы бросили взгляд на часы. Они показывают Ответ: 5.17. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин. Ответ: 0,6. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 390. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||



 .
.



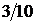


 На складе магазина имеется 10 телевизоров, среди которых 3 бракованных, что визуально не определяется. Наугад берутся 4 телевизора и подключаются к сети. Найти и построить (в виде многоугольника распределения) ряд распределе-ния числа телевизоров Х, которые будут работать. Найти математическое ожидание, дис-персию и среднее квадратичное отклонение СВ Х.
На складе магазина имеется 10 телевизоров, среди которых 3 бракованных, что визуально не определяется. Наугад берутся 4 телевизора и подключаются к сети. Найти и построить (в виде многоугольника распределения) ряд распределе-ния числа телевизоров Х, которые будут работать. Найти математическое ожидание, дис-персию и среднее квадратичное отклонение СВ Х.


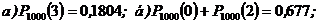



 =20 тыс. гривень в месяц и
=20 тыс. гривень в месяц и  =3,464 тыс. гривень в месяц. Найти вероятность того, что в следующем месяце она превысит 25 тыс. гривень.
=3,464 тыс. гривень в месяц. Найти вероятность того, что в следующем месяце она превысит 25 тыс. гривень.
 минут. Тогда для вас истинное время в данный момент будет случайной величиной. Найти её функцию распределения, считая, что время течёт равномерно.
минут. Тогда для вас истинное время в данный момент будет случайной величиной. Найти её функцию распределения, считая, что время течёт равномерно. .
.