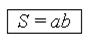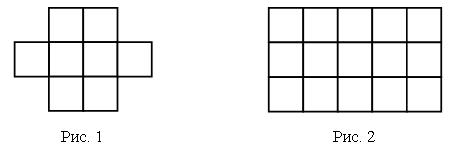
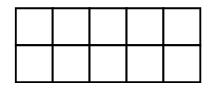
Справочный материал для учителя

Фигура на рисунке 1 состоит из 8 квадратов со стороной 1 см каждый. Площадь одного такого квадрата называют квадратным сантиметром. Пишут: 1 см². Значит, площадь всей фигуры равна 8 см².

Если какую-нибудь фигуру можно разбить на р квадратовсостороной1 см, то ее площадь равна р см².

Прямоугольник на рисунке 2 состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см. Весь прямоугольник состоит из 5 · 3 = 15 таких квадратов, и его площадь равна 15 см².

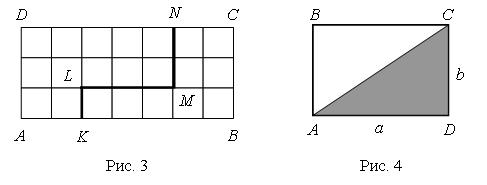
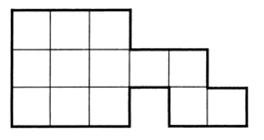
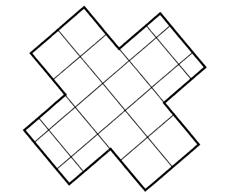
Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.

Запишем это правило в виде формулы. Площадь прямоугольника обозначим буквой S, его длину – буквой а, а ширину – буквой b.

Получаем формулу площади прямоугольника:

Две фигуры называют равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Линия KLMN на рисунке 3 разбивает прямоугольник ABCD на две части. Одна из частей имеет площадь 12 см², а другая – 9 см². Площадь всего прямоугольника равна 3 · 7, то есть 21 см². При этом 21 = 12 + 9.

Площадь всей фигуры равна сумме площадей ее частей.

Отрезок АС разбивает прямоугольник на два равных треугольника: ABC и ADC (рис. 4).

Площадь каждого треугольника равна половине площади всего прямоугольника.

· Квадратной единицей называют не квадрат, а его площадь.

· Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.

· Квадратным дециметром называют площадь квадрата с длиной стороны 1 дм.

· Квадратным метром называют площадь квадрата с длиной стороны 1 м.

! Следите за правильным применением учащимися терминологии. В быту дети довольно часто слышат, как взрослые говорят о том, что площадь такой-то комнаты или квартиры равна 15 м, 60 м и т. д. Разъясните, что в этих случаях речь идет о площадях 15 м², 60 м², а не о длинах.

– Рассмотрите рисунок на с. 23 учебника и объясните, как найти площадь фигуры. (Надо разделить фигуры на квадраты с длиной стороны 1 см и пересчитать, сколько получилось квадратов.)

Задание № 2(с. 23).

Учащиеся читают величины, записанные единицами площади.

Задание № 3(с. 23).

Выполняя задание, учащиеся устанавливают взаимосвязь между двумя изученными единицами площади: 1 дм² = 100 см².

Не следует требовать от учащихся знания наизусть этой зависимости.

Задание № 4(с. 23).

Для выполнения задания учащиеся используют палетку. Цель задания – научить детей измерять площадь фигур с помощью палетки. Сначала объясните ученикам, как надо накладывать палетку на фигуру, чтобы было удобно выполнять измерения, и только потом переходите к практической работе. Рассуждать дети должны примерно так: «В голубой фигуре ровно 13 квадратов. Площадь каждого квадрата – 1 см², значит, площадь фигуры – 13 см².

В желтой фигуре ровно 12 квадратов (их площадь – 12 см²), 6 половинок квадратов (их площадь – 3 см²) и 4 четвертинки квадрата (их площадь – 1 см²). Следовательно, площадь желтой фигуры:

12 + 3 + 1 = 16, то есть 16 см²».

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 11(с. 25).

Вывод: чтобы найти неизвестный делитель, надо делимое разделить на значение частного.

Задание № 13(с. 25).

Ответ: пятая часть, четвертая часть и две шестых части.

2. Работа в печатной тетради № 2.

Задание № 35.

Чертеж:

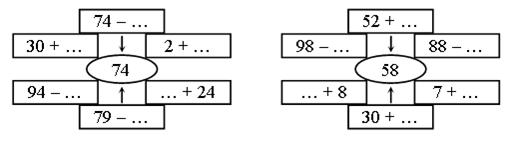
Ответ: 10 см².

Задание № 192.

Ответ: 7 см² и 8 см².

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите единицы измерения площади фигуры.

Домашнее задание: № 10, 12 (учебник); № 32, 191 (рабочая тетрадь).

Урок 65
Площадь фигуры. Единицы площади

Цели урока:продолжить формирование умений определять площадь фигуры приемом пересчитывания квадратов, на которые разделена фигура; совершенствовать навыки работы с математическими графами; развивать логическое мышление и умение рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Вставьте пропущенные числа.

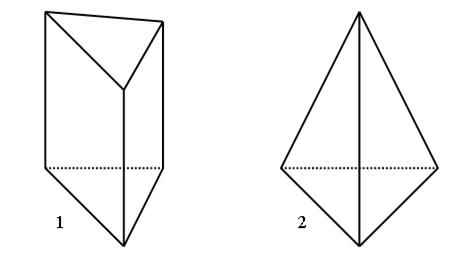
2. Задача.

Почтальон принес в наш дом 2 десятка газет и 8 журналов – в каждую квартиру что-нибудь одно. Сколько квартир получили газету или журнал?

3. Рассмотрите чертеж:

а) Какая фигура «лишняя»?

б) У какой фигуры 6 вершин, 5 граней, 9 ребер?

в) У какой фигуры только одна вершина?

г) В чем сходство и различие фигур 4 и 5?

д) Названия каких из этих фигур ты знаешь?

III. Сообщение темы урока.

– Сегодня на уроке будем определять площадь различных геометрических фигур.