Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Различные приемы интегрирования тригонометрических функций.1) Интегралы вида Рассмотрим следующие случаи: а) Если б) Если
в) Если 2) Интегралы вида С помощью универсальной тригонометрической подстановки 3) Интегралы вида Такие интегралы легко вычисляются, если применить следующие тригонометрические формулы:
Примеры 18.Вычислить интегралы: 1) Решение:Применим подстановку
2) Решение: Воспользуемся подстановкой
3) Решение: Подынтегральная функция нечетна относительно синуса, поэтому сделаем подстановку
4) Решение: Используя формулы понижения степени, получим
5) Решение: В данном случае применим подстановку
6) Решение: Представим числитель по формуле
Для нахождения первого интеграла воспользуемся универсальной тригонометрической подстановкой
Для нахождения второго интеграла воспользуемся методом интегрирования по частям. Полагая
Следовательно,
Итак, находим искомый интеграл
7) Решение: Воспользуемся универсальной тригонометрической подстановкой 
8) Решение: Воспользуемся тригонометрической формулой преобразования произведения в сумму, получим
Задания для самостоятельной работы по теме «Интегрирование тригонометрических функций». Задание. Вычислить следующие интегралы:
Тема19. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ. Различные приемы интегрирования иррациональных функций. 1) Если корни в подынтегральном выражении имеют вид то с помощью подстановки 2) Интегралы вида 3) Интегралы вида 4) Интегралы вида а) интегрируются с помощью тригонометрических подстановок: а) б) в) Примеры 19.Вычислить интегралы: 1) Решение: Здесь
Получился интеграл от рациональной дроби. Выделяем целую часть:
Для нахождения последнего интеграла разложим подынтегральную функцию на простейшие дроби:
откуда
Приравнивая коэффициенты при одинаковых степенях
2) Решение: Полагая
3) Решение: Положим Следовательно,
Для вычисления полученного интеграла представим подынтегральную дробь в виде
Таким образом,
4) Решение: Положим
Так как 5) Решение: Полагаем
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 234. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,где
,где  и
и  − целые числа.
− целые числа. − нечетное число, то применяется подстановка
− нечетное число, то применяется подстановка  ;
;  − нечетное число, то применяется подстановка
− нечетное число, то применяется подстановка  .
. и
и  − четные неотрицательные числа, то подынтегральное выражение преобразуют с помощью формул понижения степени:
− четные неотрицательные числа, то подынтегральное выражение преобразуют с помощью формул понижения степени: ,
,  ,
,  .
.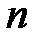 и
и  − либо оба четные, либо оба нечетные, причем хотя бы один из них отрицателен, то применяют подстановку
− либо оба четные, либо оба нечетные, причем хотя бы один из них отрицателен, то применяют подстановку  .
. , где
, где  − рациональная функция.
− рациональная функция. , откуда
, откуда  ,
,  ,
, 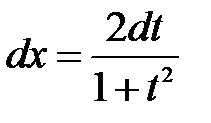 , интегралы рассматриваемого вида приводятся к интегралам от рациональных алгебраических функций.
, интегралы рассматриваемого вида приводятся к интегралам от рациональных алгебраических функций. ,
,  ,
,  .
. ,
,  ,
, .
. .
. и воспользуемся формулой
и воспользуемся формулой  . Тогда
. Тогда

 .
. . Имеем
. Имеем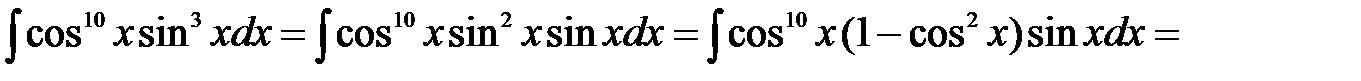


 .
. . Тогда
. Тогда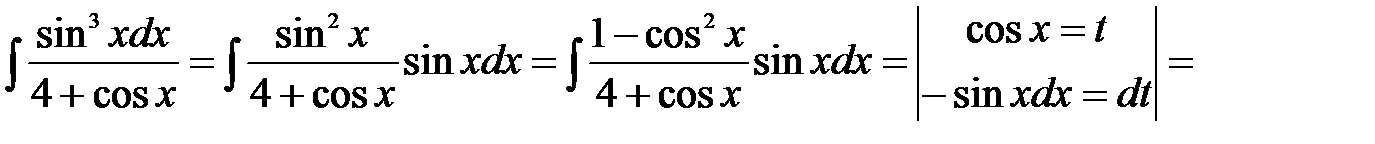


 .
.


 .
. и формулу
и формулу  . Тогда
. Тогда
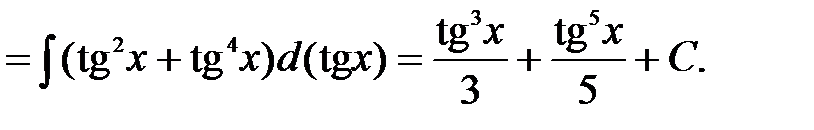
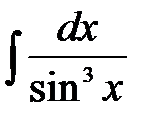 ,
, и разделим почленно числитель на знаменатель, получим
и разделим почленно числитель на знаменатель, получим .
. , имеем
, имеем
 ,
,  , имеем
, имеем ,
,  .
.

 ,
, . Имеем
. Имеем
 .
. .
.

 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
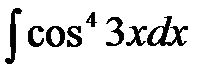 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

 ,
, , где
, где  − наименьшее общее кратное показателей корней, т.е. чисел
− наименьшее общее кратное показателей корней, т.е. чисел  , подынтегральное выражение преобразуется в рациональную дробь.
, подынтегральное выражение преобразуется в рациональную дробь. преобразуются в интегралы от рациональных дробей с помощью подстановки
преобразуются в интегралы от рациональных дробей с помощью подстановки  .
. рационализируются с помощью подстановки
рационализируются с помощью подстановки  .
. ,б)
,б)  ,в)
,в) 
 или
или  ,
,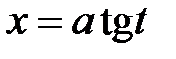 или
или  ,
, или
или  .
. .
. входит в подынтегральную функцию с показателями корней 2 и 3. Поэтому применяем подстановку
входит в подынтегральную функцию с показателями корней 2 и 3. Поэтому применяем подстановку  , откуда
, откуда .
. .
. ,
, .
. , находим
, находим  Следовательно,
Следовательно,


 ,
, , имеем
, имеем

 где
где  .
.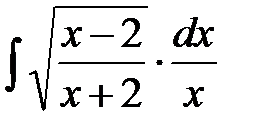 .
. , откуда
, откуда  ,
,  .
. .
. .
.
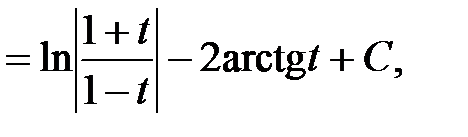 где
где  .
.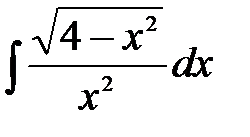 .
. . Тогда
. Тогда  ,
, 
 . Имеем
. Имеем
 , то
, то  ,
,  . Поэтому
. Поэтому 
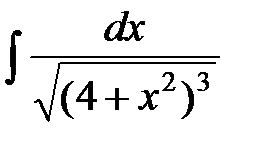 .
. . Откуда
. Откуда  ,
, 
 . Следовательно,
. Следовательно,