
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теоремы о среднем дифференциального исчисления.1. Теорема Ролля.Если функция 1)непрерывна на отрезке 2)дифференцируема на интервале 3) то найдется по крайней мере одна точка 2. Теорема Лагранжа.Если функция 1. непрерывна на отрезке 2. дифференцируема на интервале то на интервале
3. Теорема Коши.Если две функции 1. непрерывны на отрезке 2. дифференцируемы на интервале 3. то на интервале
Замечание 11.1.Формулу из теоремы Лагранжа иногда, обозначая
Формула Тейлора. Естественным обобщением последней формулы для функций, имеющих nпроизводных в некоторой окрестности точки
где
( Пример 11.2.Проверить справедливость теоремы Лагранжа для функции Решение: Функция
Решая данное уравнение относительно Правило Лопиталя. Простым приемом для раскрытия неопределенностей вида Теорема 11.1.Предел отношения двух бесконечно малых или бесконечно больших функций 
Пример 11.3. Вычислить Решение: Подстановка предельного значения
Замечание 11.2.Если
Пример 11.4. Вычислить Решение: Подстановка предельного значения приводит к неопределенности вида
Замечание 11.3.Если
Пример 11.5. Вычислить Решение: Подстановка предельного значения приводит к неопределенности вида
Замечание 11.4.При отыскании предела функции вида
а в силу непрерывности показательной функции:
Пример 11.6. Вычислить Решение: Подстановка предельного значения приводит к неопределенности вида
Тогда |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 196. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 :
: ,
, ,
, ,
,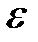 на интервале
на интервале  , в которой
, в которой 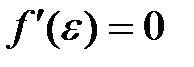 .
. :
: , в которой
, в которой .
. и
и  :
: на интервале
на интервале 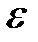 , в которой
, в которой .
. , записывают в следующем виде:
, записывают в следующем виде: .
. (включая саму эту точку), является формула Тейлора:
(включая саму эту точку), является формула Тейлора:
 – остаточный член формулы Тейлора, в форме Лагранжа имеющий вид:
– остаточный член формулы Тейлора, в форме Лагранжа имеющий вид:
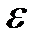 – некоторая промежуточная точка между точками
– некоторая промежуточная точка между точками  и
и  ).
). на отрезке
на отрезке  .
. определена и непрерывна на отрезке
определена и непрерывна на отрезке  как элементарная функция. Найдем ее производную:
как элементарная функция. Найдем ее производную:  , т.е. функция дифференцируема на интервале
, т.е. функция дифференцируема на интервале 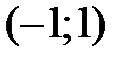 . Следовательно, теорема Лагранжа справедлива для функции
. Следовательно, теорема Лагранжа справедлива для функции  на отрезке
на отрезке  найдется по крайней мере одна точка
найдется по крайней мере одна точка  , в которой
, в которой .
. , получим
, получим  .
. и
и  при отыскании предела функций является правило Лопиталя (Гильом Лопиталь (1661-1704) – французский математик).
при отыскании предела функций является правило Лопиталя (Гильом Лопиталь (1661-1704) – французский математик). и
и  равен пределу отношения их производных, если последний существует, т.е.
равен пределу отношения их производных, если последний существует, т.е. .
. .
. приводит к неопределенности вида
приводит к неопределенности вида  . Предел отношения производных существует. Тогда
. Предел отношения производных существует. Тогда .
. и
и  при
при  , то отыскание предела
, то отыскание предела  (неопределенность вида
(неопределенность вида  ) может быть сведено к одному из ранее рассмотренных случаев
) может быть сведено к одному из ранее рассмотренных случаев  или
или 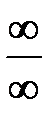 путем тождественных преобразований:
путем тождественных преобразований: или
или  .
. .
. . Преобразуем функцию так, чтобы получилась неопределенность вида
. Преобразуем функцию так, чтобы получилась неопределенность вида  :
:  . Предел отношения производных существует. Тогда
. Предел отношения производных существует. Тогда .
. и
и  при
при  , тоотыскание предела
, тоотыскание предела  (неопределенность вида
(неопределенность вида  ) может быть сведено к раскрытию неопределенности вида
) может быть сведено к раскрытию неопределенности вида  путем тождественных преобразований:
путем тождественных преобразований: или
или  .
.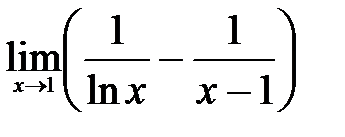 .
.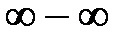 . Преобразуем функцию так, чтобы получилась неопределенность вида
. Преобразуем функцию так, чтобы получилась неопределенность вида  :
:  . Предел отношения производных существует. Тогда
. Предел отношения производных существует. Тогда
 могут возникнуть неопределенности вида
могут возникнуть неопределенности вида 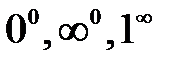 . В этих случаях можно прийти к неопределенности вида
. В этих случаях можно прийти к неопределенности вида  путем следующих преобразований:
путем следующих преобразований: ,
,
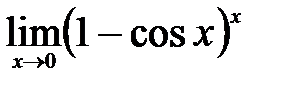 .
. . Преобразуем исходный предел:
. Преобразуем исходный предел:  , где
, где
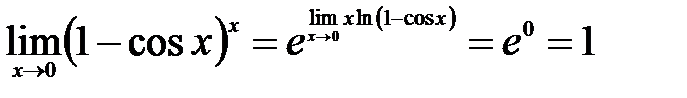 .
.