
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задания для самостоятельной работыпо теме«Исследование функций и построение графиков». Задание 1.Определить интервалы монотонности функций:
Задание 2.Найти точки экстремума функций:
Задание 3.Определить наибольшее и наименьшее значение функции на отрезке:
Задание 4.Найти точки перегиба и характер выпуклости графика функции:
Задание 5.Найти уравнение асимптот кривых:
Задание 6.Исследовать функции и построить их графики:
Тема 13. ПЕРВООБРАЗНАЯ ФУНКЦИИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. Понятие первообразной и неопределенного интеграла. Определение 13.1.Функция
Любая непрерывная функция Определение 13.2.Совокупность всех первообразных Определение 13.3.Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Основные свойства неопределенного интеграла.  1. Производная неопределенного интеграла равна подынтегральной функции: 2. Дифференциал от неопределенного интеграла равен подынтегральной функции: 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
4. Постоянный множитель можно выносить за знак интеграла:
5. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций:
6. Инвариантность неопределенного интеграла: формула для неопределенного интеграла остается справедливой независимо от того, явялется ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную, т.е. если Таблица интегралов.
Метод непосредственного интегрирования. Метод непосредственного интегрирования основан на приведении вычисляемого интеграла к одному из табличных интегралов путем тождественных преобразований подынтегральной функции (или выражения) и применения основных свойств неопределенного интеграла. Примеры 13.Вычислить интегралы: 1) Решение: Разделим почленно числитель на знаменатель. В результате подынтегральная функция разложится на слагаемые, каждое из которых можно проинтегрировать, используя основные свойства неопределенного интеграла:
2) Решение: Выделим целую часть в подынтегральной дроби путем прибавления и вычитания в числителе числа 4, в результате получим
3) Решение: Раскроем квадрат разности в подынтегральной функции и проинтегрируем каждое слагаемое, имеем
4) Решение: В данном примере воспользуемся известной тригонометрической формулой
В результате получим
5) Решение: Воспользуемся свойством 6 неопределенного интеграла, где
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 227. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
 .
.
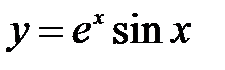 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 ,
,  .
.
 ,
,  .
.
 ,
, 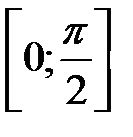 .
.
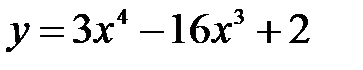 ,
,  .
.
 ,
,  .
.

 .
.
 .
.
 .
.
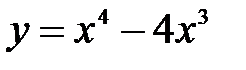 .
.
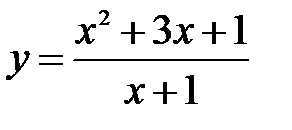 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
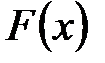 называется первообразной функции
называется первообразной функции  на некотором интервале, если для любого
на некотором интервале, если для любого  из этого интервала выполняется равенство
из этого интервала выполняется равенство .
. имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.
имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.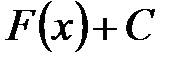 , где
, где  − произвольная постоянная, называется неопределенным интегралом и обозначается следующим образом:
− произвольная постоянная, называется неопределенным интегралом и обозначается следующим образом:  .Здесь
.Здесь  – подынтегральным выражением,
– подынтегральным выражением,  – переменной интегрирования.
– переменной интегрирования. .
. .
.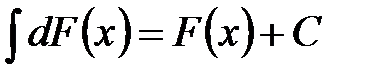 .
. .
. .
. и
и 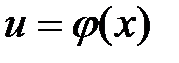 – произвольная функция, имеющая непрерывную производную, то
– произвольная функция, имеющая непрерывную производную, то  .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
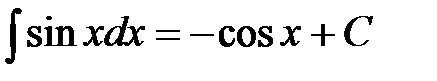 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
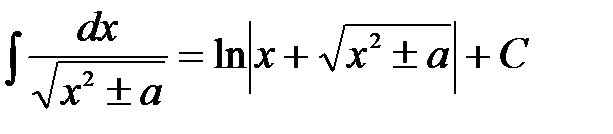 .
.
 .
.
 .
.
 .
. .
. .
. .
. .
. .
. , имеем
, имеем .
.