
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задания для самостоятельной работыпо теме«Приложения дифференциального исчисления». Задание 1.Найти приближенное значение:
Задание 2.Вывести приближенную формулу (при условии, что Задание 3.Используя теорему Ролля, доказать, что для многочлена Задание 4.Получить разложение основных элементарных функций в окрестности точки 0:
Задание 5.Используя разложение соответствующей функции из задания 4, вычислить приближенное значение с точностью до 0,001:
Задание 6.Вычислить пределы следующих функций, используя правило Лопиталя:
Тема 12. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ. Возрастание и убывание функции. Определение 12.1.Функция
Определение 12.2.Функция
Перечисленные выше условия называются условиями монотонности в широком смысле. Если в них знак равенства исключен, то функция Теорема 12.1.Дифференцируемая функция
и является монотонно убывающей, если
Пример 12.1. Найти интервалы монотонности функции Решение: Вычисляем производную:  Экстремумы функции. Определение 12.3.Точка Определение 12.4.Точка Значения функции Необходимое условие существования экстремума. Для того чтобы функция Определение 12.5.Точки, в которых выполнено необходимое условие экстремума и которые входят в область определения функции, называются критическими. Достаточное условие экстремума. Если при переходе через точку Схема исследования функции 1. Найти производную 2. Найти критические точки функции, в которых производная 3. Исследовать изменение знака производной при переходе через критическую точку. Сделать вывод о наличии экстремума. 4. Найти экстремумы функции (значения функции в точках экстремума). Пример 12.2. Определить точки экстремума функции Решение: 1. Найдем производную заданной функции:
2. Найдем точки, в которых производная равна нулю – производная не существует – таких точек нет. Значит, критическими являются точки 3. Исследуем изменение знака производной при переходе через критическиеточки: при Таким образом, |
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 204. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 мало по сравнению с
мало по сравнению с  ):
):  .
. на интервале
на интервале  найдется корень уравнения
найдется корень уравнения  .
. .
.
 .
.
 .
.
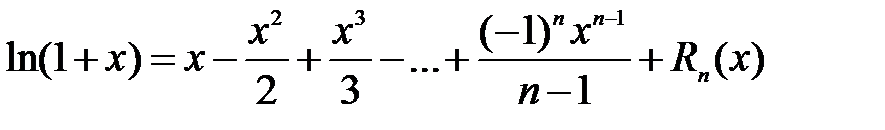 .
.
 .
.
 .
.
 .
.
 .
.
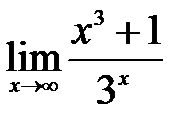 .
.
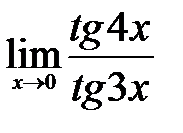 .
.
 .
.

 .
.
 .
.

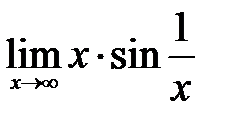 .
.
 .
.

 .
.
 .
.

 .
.
 .
.
 .
.
 .
.
 .
.
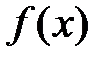 называется монотонно возрастающей на интервале
называется монотонно возрастающей на интервале 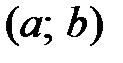 , если для любых
, если для любых  из этого интервала выполнено условие
из этого интервала выполнено условие при
при 
 называется монотонно убывающей на интервале
называется монотонно убывающей на интервале  , если для любых
, если для любых  из этого интервала выполнено условие
из этого интервала выполнено условие при
при 
 называется строго монотонной.
называется строго монотонной. является монотонно возрастающей на интервале
является монотонно возрастающей на интервале 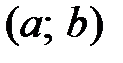 тогда и только тогда, когда
тогда и только тогда, когда при
при 
 при
при 
 .
. . Очевидно,
. Очевидно,  при
при  и
и  при
при  , т.е. функция убывает на интервале
, т.е. функция убывает на интервале  и возрастает на интервале
и возрастает на интервале  .
. называется точкой максимумафункции
называется точкой максимумафункции  , если в некоторой окрестности этой точкивыполняется неравенство
, если в некоторой окрестности этой точкивыполняется неравенство  .
. называется точкой минимумафункции
называется точкой минимумафункции  , если в некоторой окрестности этой точки выполняется неравенство
, если в некоторой окрестности этой точки выполняется неравенство  .
. в точках
в точках 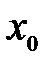 и
и  называются соответственно максимумом и минимумом этой функции, объединяемые общим названием экстремумы функции.
называются соответственно максимумом и минимумом этой функции, объединяемые общим названием экстремумы функции. имела экстремум в точке
имела экстремум в точке  , необходимо, чтобы ее производная в этой точке равнялась нулю (
, необходимо, чтобы ее производная в этой точке равнялась нулю (  ) или не существовала.
) или не существовала. производная дифференцируемой функции
производная дифференцируемой функции  меняет свой знак с «плюса» на «минус», то точка
меняет свой знак с «плюса» на «минус», то точка  есть точка максимума функции
есть точка максимума функции 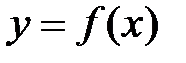 , а если с «минуса»на «плюс»– то точка минимума. Если изменения знака производной не происходит, то экстремума нет.
, а если с «минуса»на «плюс»– то точка минимума. Если изменения знака производной не происходит, то экстремума нет. на экстремум:
на экстремум: .
. =0 или не существует.
=0 или не существует. .
. .
. =0:
=0:  при
при  и
и  ;
; и
и  .
.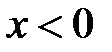
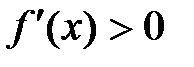 , при
, при 
 ,при
,при 
 .
. – точка максимума, а
– точка максимума, а 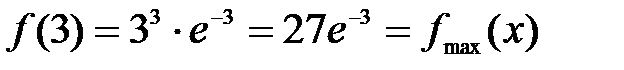 – максимум функции.
– максимум функции.