
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегрирование неправильных рациональных дробей.Для нахождения интеграла от неправильной рациональной дроби
где Примеры 17.Вычислить интегралы: 1) Решение:Представим подынтегральную функцию в виде суммы простейших дробей, т.е.
Приводя дроби в правой части равенства к общему знаменателю и приравнивая после этого числители правой и левой частей, получим
Полагая в полученном тождестве Полагая Таким образом, искомый интеграл
2) Решение: Под интегралом стоит правильная рациональная дробь. Разлагая ее на сумму простейших дробей, получим
Приведем правую часть полученного соотношения к общему знаменателю:
Для нахождения неопределенных коэффициентов будем комбинировать два вышеизложенных способа. Полагая При Для определения коэффициента В результате находим искомый интеграл:
3) Решение: Представим подынтегральную функцию в виде суммы простейших дробей.
Приводя правую часть равенства к общему знаменателю и приравнивая числители, получаем
Полагая Коэффициенты при при при Решив полученную систему, получим Следовательно,
В последнем интеграле квадратный трехчлен 
Тогда
Таким образом, имеем
4) Решение: Квадратный трехчлен
Следовательно,
Приравниваем коэффициенты при одинаковых степенях при при при при Решив полученную систему, получим
Для нахождения последнего интеграла воспользуемся ранее указанной рекуррентной формулой:
Итак, находим искомый интеграл:
5) Решение: Под интегралом стоит неправильная рациональная дробь. Выделяя целую часть, получим
Следовательно,
Первый интеграл интегрируется непосредственно
Во втором интеграле замечая, что
на простейшие дроби:
Приводя к общему знаменателю и приравнивая числители, получаем
Полагая Для нахождения коэффициента Поэтому
Наконец, находим искомый интеграл
Задания для самостоятельной работы по теме «Интегрирование рациональных дробей». Задание. Найти интегралы от рациональных дробей:
Тема18. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ. |
||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 212. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
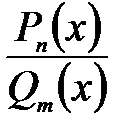 следует выделить из нее целую часть, т.е. представить в виде
следует выделить из нее целую часть, т.е. представить в виде
 − многочлен (целая часть при делении);
− многочлен (целая часть при делении); 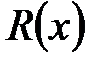 − остаток от деления. Очевидно, что второе слагаемое есть уже правильная рациональная дробь.
− остаток от деления. Очевидно, что второе слагаемое есть уже правильная рациональная дробь. .
. .
. .
. , имеем
, имеем  .
. , имеем
, имеем  .
. .
. .
. .
. .
.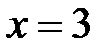 , получим
, получим  .
. имеем
имеем  .
. приравняем коэффициенты при
приравняем коэффициенты при  в обеих частях тождества:
в обеих частях тождества:  , откуда
, откуда  .
. .
. .
.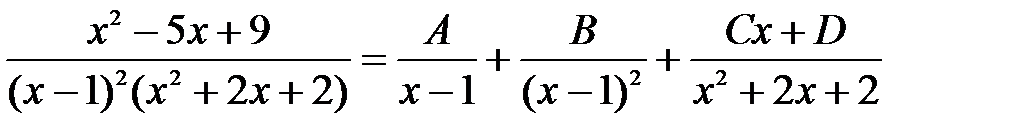 .
. .
. , находим
, находим  :
: 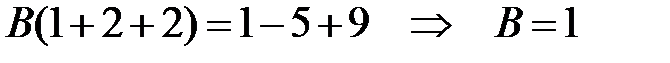 .
. найдем, приравнивая коэффициенты при
найдем, приравнивая коэффициенты при  ,
,  и свободные члены в тождестве:
и свободные члены в тождестве: :
:  ;
; :
:  ;
; :
:  .
. ,
,  ,
,  .
. .
. не имеет действительных корней. Для его вычисления выделяем полный квадрат из квадратного трехчлена, стоящего в знаменателе.
не имеет действительных корней. Для его вычисления выделяем полный квадрат из квадратного трехчлена, стоящего в знаменателе. .
.

 .
. .
. .
. не имеет действительных корней. Поэтому подынтегральная дробь раскладывается на слагаемые следующим образом:
не имеет действительных корней. Поэтому подынтегральная дробь раскладывается на слагаемые следующим образом: .
. .
. :
: :
: 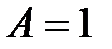 ;
; :
:  ;
; :
:  ;
; :
:  .
.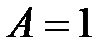 ,
,  ,
, 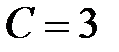 ,
,  . Следовательно,
. Следовательно,


 .
. .
.
 .
. .
. .
. .
.
 , разложим правильную рациональную дробь
, разложим правильную рациональную дробь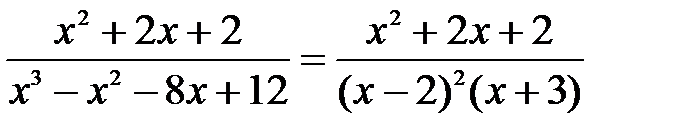
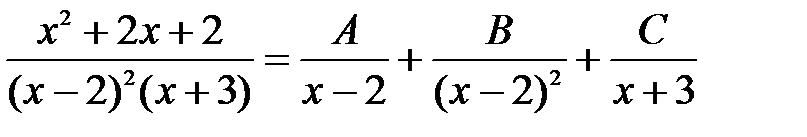 .
. .
. и
и 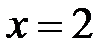 , находим
, находим  и
и  .
. приравняем коэффициенты при
приравняем коэффициенты при 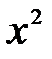 в тождестве. Получим
в тождестве. Получим  .
.
 .
. .
. .
.
 .
.

 .
.
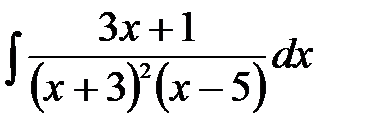 .
.
 .
.
 .
.
 .
.

 .
.

 .
.