
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задания для самостоятельной работыпо теме«Первообразная функции. Неопределенный интеграл». Задание. Методом непосредственного интегрирования найти следующие интегралы:
Тема14. ИНТЕГРИРОВАНИЕ МЕТОДОМ ПОДСТАНОВКИ. Замена переменной и подведение под знак дифференциала. Замена переменной в неопределенном интеграле производится с помощью подстановок двух типов: 1)
Функцию 2)
Такого рода преобразование называют подведением под знак дифференциала. Примеры 14.Вычислить интегралы: 1) Решение: Данный интеграл окажется табличным, если под знаком дифференциала будет стоять аргумент
2) Решение: Так как
3) Решение: Замечаем, что
4) Решение: Поскольку
5) Решение: Применим подстановку
6) Решение: Используем подстановку
Задания для самостоятельной работы по теме «Интегрирование методом подстановки». Задание. Методом подстановки найти следующие интегралы:
Тема15.ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ.  Формула интегрирования по частям. Если
Данная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла При нахождении интегралов типа
за
за Примеры 15.Вычислить интегралы: 1) Решение: Воспользуемся формулой интегрирования по частям:
2) Решение: Воспользуемся формулой интегрирования по частям:
3) Решение: Воспользуемся формулой интегрирования по частям:
4) Решение: Воспользуемся формулой интегрирования по частям, получим:
К последнему интегралу снова применим формулу интегрирования по частям:
Подставляя найденное выражение в первоначальное выражение, имеем
5) Решение: Воспользуемся формулой интегрирования по частям:
Последний интеграл сновапроинтегрируем раз по частям:
Таким образом,
В правой части последнего соотношения стоит искомый интеграл
Откуда
Задания для самостоятельной работы по теме «Интегрирование по частям». Задание. Проинтегрировать по частям следующие интегралы:
Тема16. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 234. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
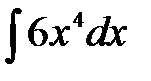 .
.
 .
.
 .
.

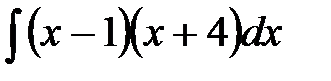 .
.
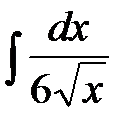 .
.
 .
.
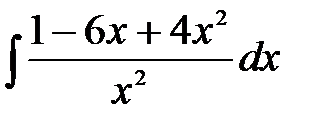 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

 .
.
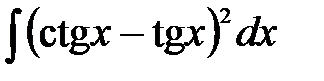 .
.
 .
.
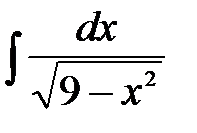 .
.
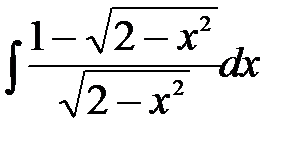 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 , где
, где  − новая переменная;
− новая переменная;  − непрерывно дифференцируемая функция. В этом случае формула замены переменной имеет вид
− непрерывно дифференцируемая функция. В этом случае формула замены переменной имеет вид .
. стараются выбрать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.
стараются выбрать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид. , где
, где  − новая переменная. Тогда формула замены переменной приобретает вид
− новая переменная. Тогда формула замены переменной приобретает вид .
. .
.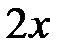 подынтегральной функции
подынтегральной функции  . Так как
. Так как  , то
, то .
. .
. , то
, то .
. .
. . Тогда
. Тогда .
.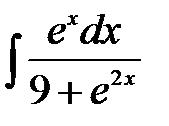 .
. , имеем
, имеем .
.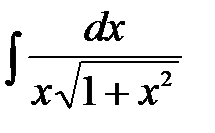 .
.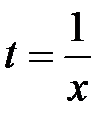 , тогда
, тогда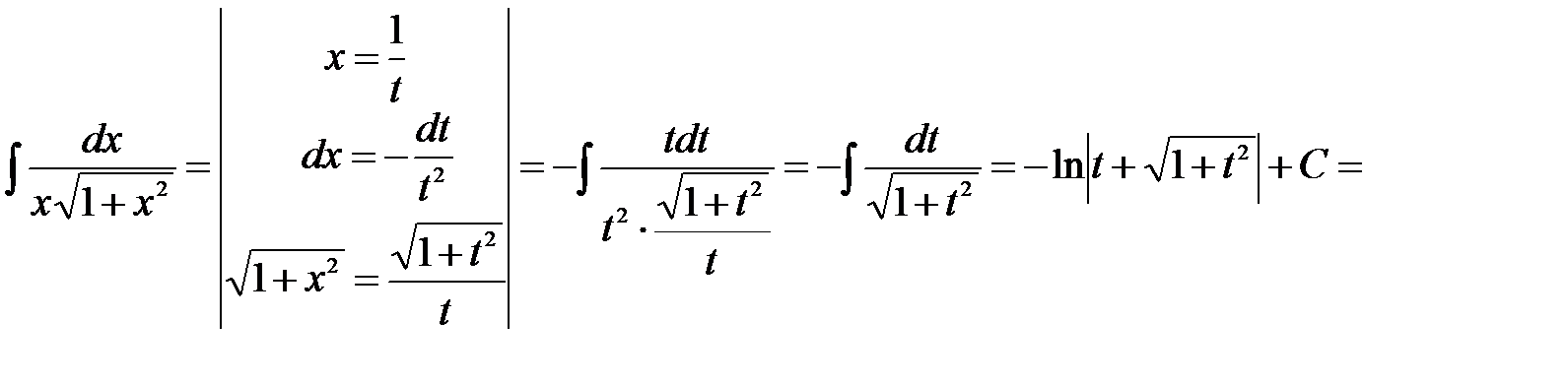
 .
. .
. . Следовательно, получим
. Следовательно, получим
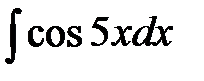 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
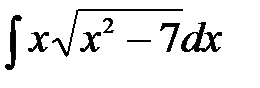 .
.
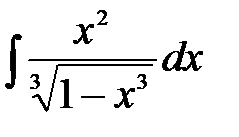 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
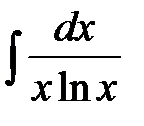 .
.
 .
.
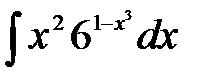 .
.
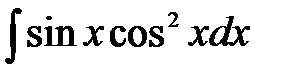 .
.
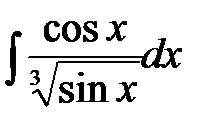 .
.
 .
.
 .
.
 .
.
 .
.

 .
.
 .
.
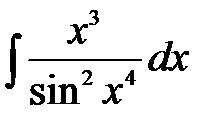 .
.
 .
.
 .
.
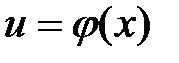 и
и  − дифференцируемые функции, то справедливо
− дифференцируемые функции, то справедливо .
.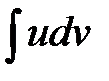 к вычислению интеграла
к вычислению интеграла  , который оказывается более простым.
, который оказывается более простым. ,
,  ,
, 
 следует принять многочлен
следует принять многочлен  , а за
, а за 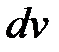 − соответственно выражения
− соответственно выражения  ,
,  ,
,  ; при отыскании интегралов вида
; при отыскании интегралов вида ,
,  ,
, 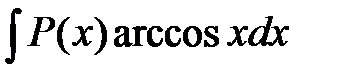 ,
, ,
, 
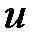 принимаются соответственно функции
принимаются соответственно функции  ,
,  ,
,  ,
,  ,
,  , а за
, а за  − выражение
− выражение 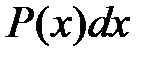 .
. .
. .
. .
.
 .
. .
. 
 .
. .
.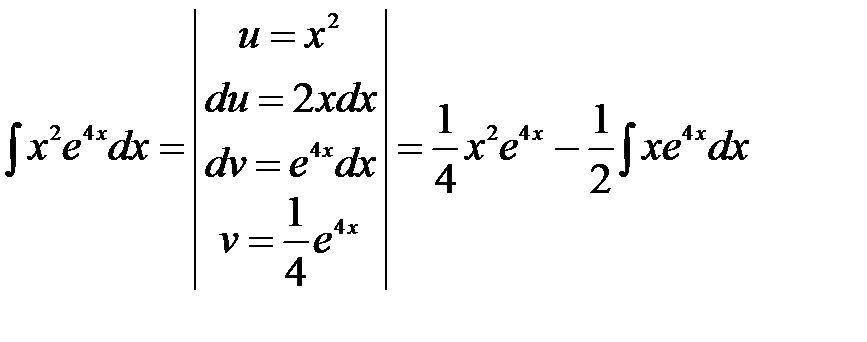 .
.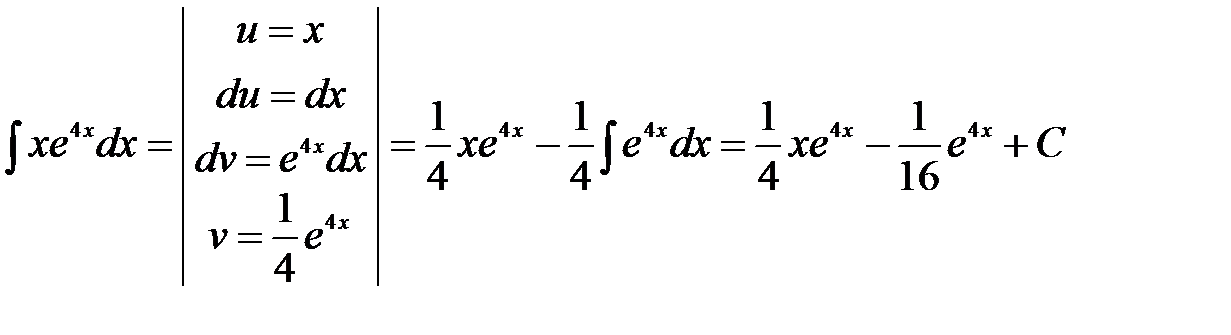 .
. .
. .
.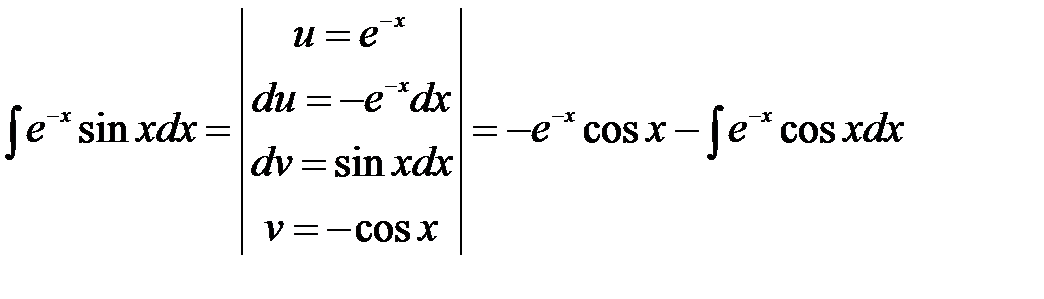 .
. .
.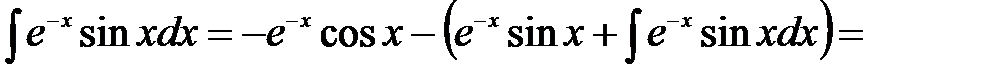
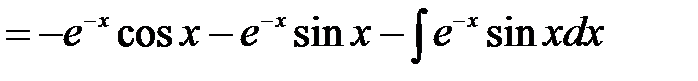 .
.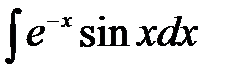 . Перенося его в левую часть, получим
. Перенося его в левую часть, получим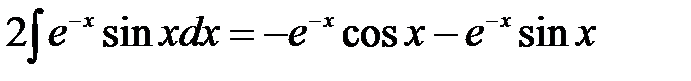 .
. .
.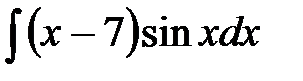 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
