
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные теоремы о непрерывных функциях.1.Сумма, разность, произведение и частное двух непрерывных функций есть непрерывная функция (для частного за исключением тех значений аргумента, в которых делитель равен нулю). 2. Если функция 3. Если функция 4. Все основные элементарные функции непрерывны в каждой точке своей области определения. Свойства функций, непрерывных на отрезке. 1. I теорема Больцано-Коши:Если функция 2. II теорема Больцано-Коши:Если функция 3. I теорема Вейерштрасса: Если функция 4. II теорема Вейерштрасса: Если функция Задания для самостоятельной работыпо теме «Непрерывность функции». Задание 1.Пользуясь определением, доказать непрерывность функции
Задание 2.Доказать, что функция
Задание 3. Исследовать на непрерывность и построить график функции 
Задание 4.Исследовать на непрерывностьфункцию
Задание 5.Найти все точки разрыва данной функции
Задание 6. Исследовать на непрерывность функцию
Задание 7.Исследовать на непрерывность функцию
Задание 8. При каком значении параметра
Тема 8. ПРОИЗВОДНАЯ ФУНКЦИИ. Понятие производной. Пусть функция Определение 8.1. Производной функции
Производная функции имеет несколько обозначений: Пример 8.1.Используя определение, доказать, что Решение: Найдем приращение функции
Тогда Определение 8.2.Операция отыскания производной данной функции называется дифференцированием этой функции. Определение 8.3.Функция, имеющая в точке |
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 312. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 непрерывна в точке
непрерывна в точке 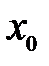 , а функция
, а функция 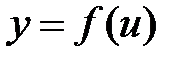 непрерывна в точке
непрерывна в точке 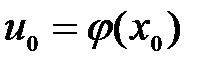 , то сложная функция
, то сложная функция 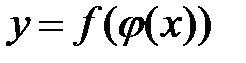 также непрерывна в точке
также непрерывна в точке  .
. непрерывна и строго монотонна на
непрерывна и строго монотонна на 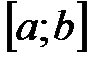 оси
оси 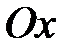 , то обратная функция
, то обратная функция 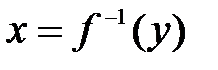 также непрерывна и монотонна на соответствующем отрезке
также непрерывна и монотонна на соответствующем отрезке 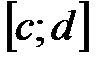 оси
оси 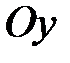 .
.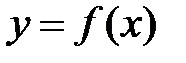 непрерывна на отрезке
непрерывна на отрезке 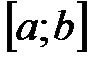 и на концах отрезка имеет значения разных знаков, то существует хотя бы одна точка
и на концах отрезка имеет значения разных знаков, то существует хотя бы одна точка 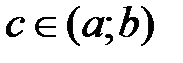 , в которой данная функция
, в которой данная функция 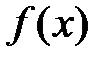 обращается в нуль:
обращается в нуль: 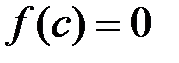 .
.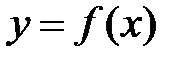 непрерывна на отрезке
непрерывна на отрезке 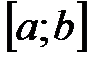 и принимает на его концах значения
и принимает на его концах значения 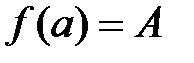 и
и 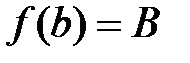 (
( 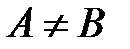 ), то найдется хотя бы одна внутренняя точка
), то найдется хотя бы одна внутренняя точка 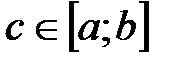 , что для любого числа
, что для любого числа 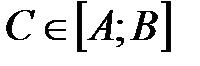 выполняется равенство
выполняется равенство 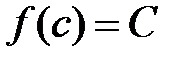 .
.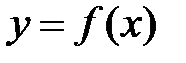 непрерывна на отрезке
непрерывна на отрезке 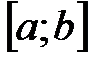 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.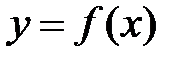 непрерывна на отрезке
непрерывна на отрезке 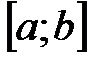 , то она достигает на этом отрезке своего наибольшего и наименьшего значений.
, то она достигает на этом отрезке своего наибольшего и наименьшего значений.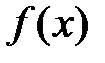 в каждой точке
в каждой точке 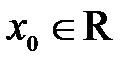 :
: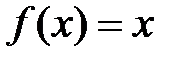 .
.
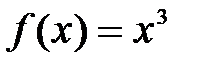 .
.
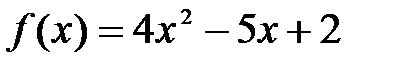 .
.
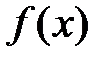 не является непрерывной в определенной точке
не является непрерывной в определенной точке 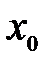 . Построить график функции
. Построить график функции 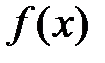 .
.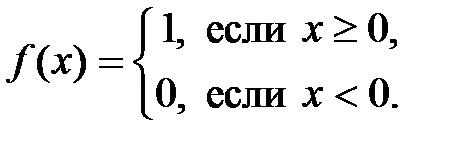
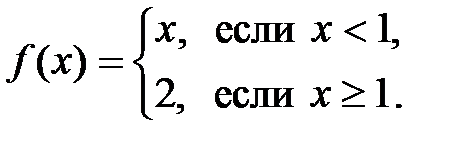
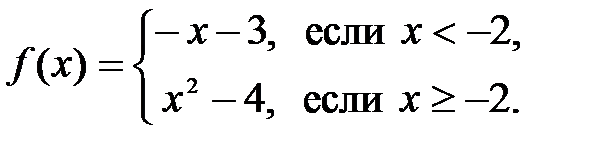
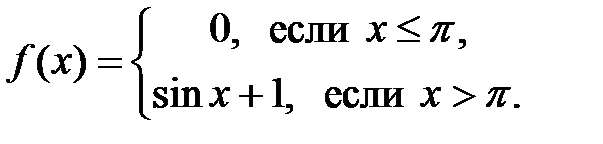
 . Найти скачок функции в точках разрыва.
. Найти скачок функции в точках разрыва.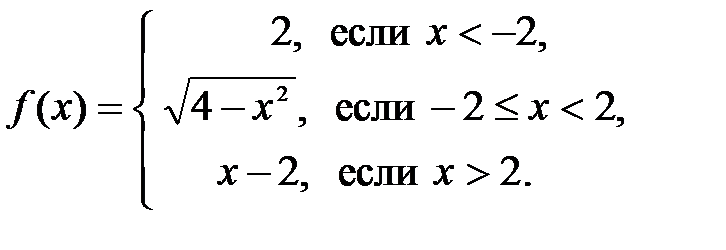
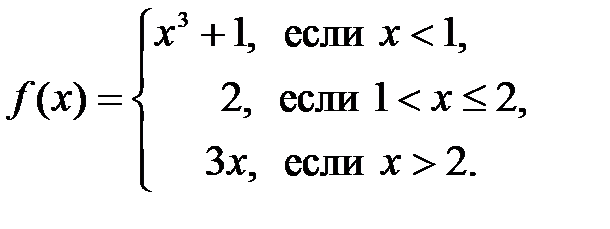
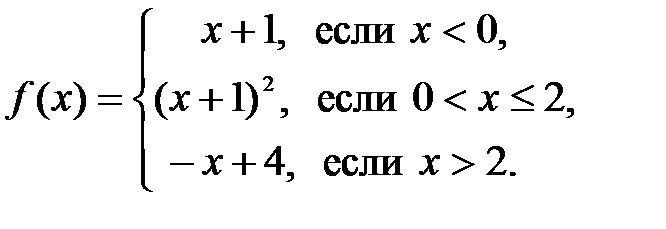
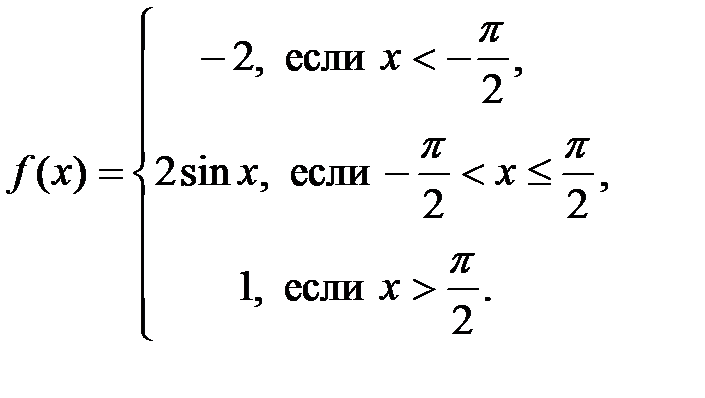
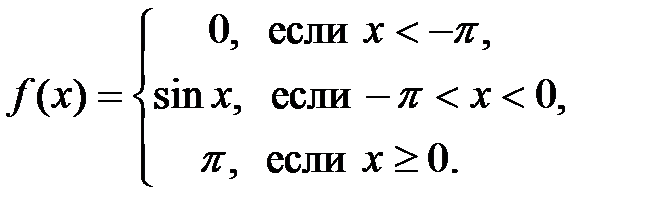
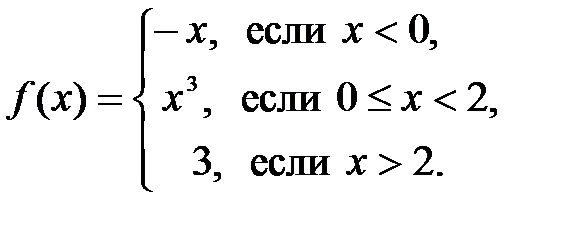
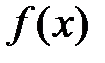 в точке
в точке 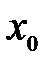 :
:  .
.
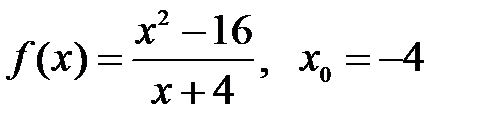 .
.
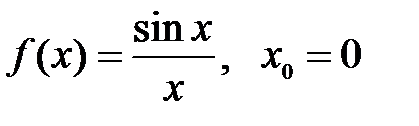 .
.
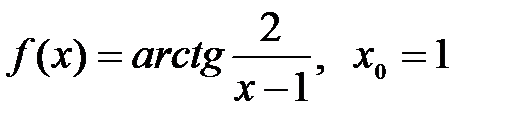 .
.
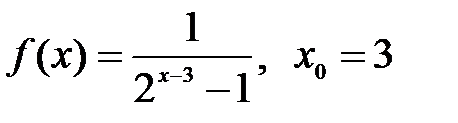 .
.
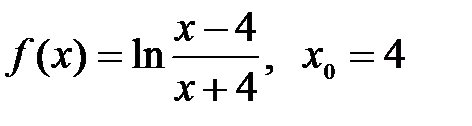 .
.
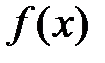 :
: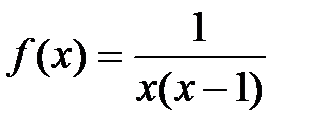 .
.
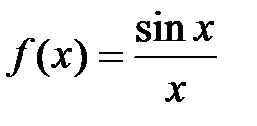 .
.
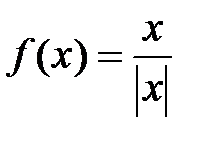 .
.
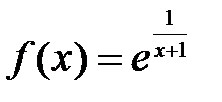 .
.
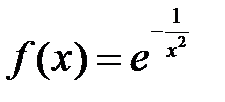 .
.
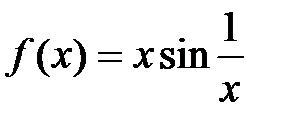 .
.
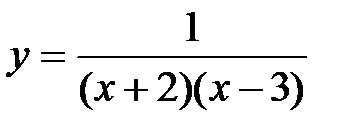 на отрезке
на отрезке  , если:
, если: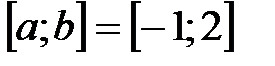 .
.
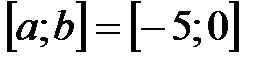 .
.
 .
.
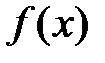 на отрезках
на отрезках 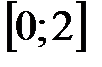 ,
, 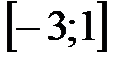 и
и 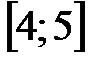 , если:
, если: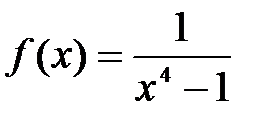 .
.
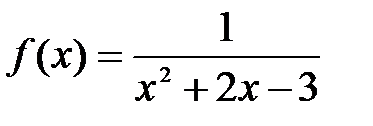 .
.
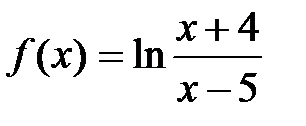 .
.
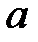 функция
функция 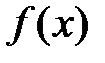 будет непрерывной:
будет непрерывной: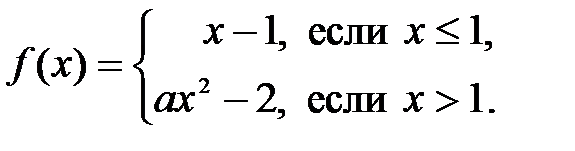
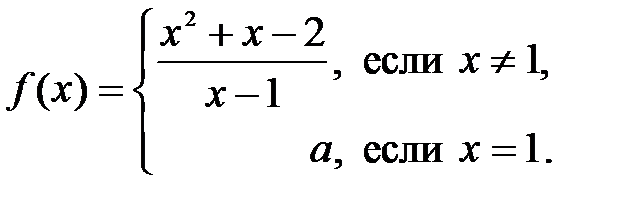
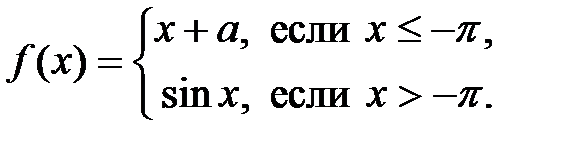
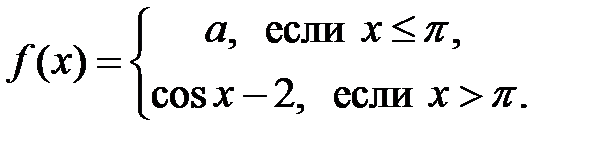
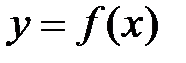 определена на интервале
определена на интервале 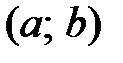 . Выберем произвольную точку
. Выберем произвольную точку 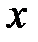 из этого интервала и зададим значению
из этого интервала и зададим значению 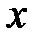 приращение
приращение 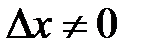 . Тогда функция получит соответствующее ему приращение
. Тогда функция получит соответствующее ему приращение 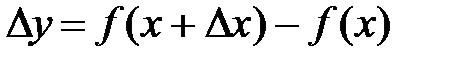 .
.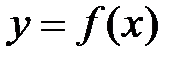 в точке
в точке 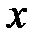 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует), т.е.
называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует), т.е.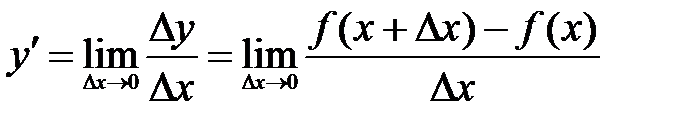 .
.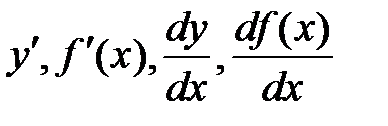 .
.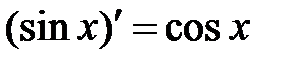 .
.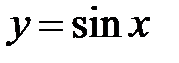 в точке
в точке  .
.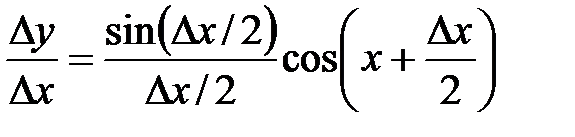 , где
, где 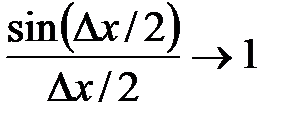 при
при 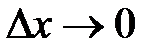 (попервому замечательному пределу),
(попервому замечательному пределу), 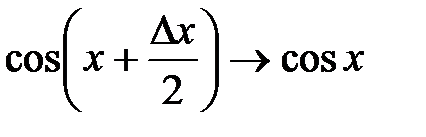 (из-за непрерывности функции
(из-за непрерывности функции 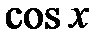 ). Таким образом,
). Таким образом, 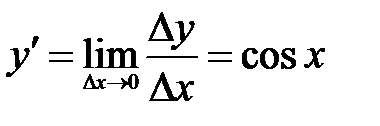 .
.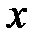 производную, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала
производную, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала 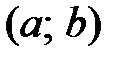 , называется дифференцируемой на этом интервале.
, называется дифференцируемой на этом интервале.