
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Простейшие типы дифференциальных уравнений первого порядка.1) Уравнение с разделёнными переменными
или
Решая первое уравнение, получим Интегрируя, найдём общее решение Решая второе, получим Интегрируя, найдём общее решение. 2) Уравнение с разделяющимися переменными,
или
Разделим обе части первого уравнения
Для второго уравнения: разделим обе части на произведение
Операция деления уравнения на произведение При делении на произведение
Определяя из этого уравнения решения
Пример 17 Решить уравнение Решение: Разделим уравнение на произведение
Интегрируя, получим общий интеграл:
В этом уравнении
Пример 18 Найти общее решение Решение:
интегрируя, найдем общее решение
3) Однородные уравнения. Функция
Если функции Однородное уравнение всегда можно привести к виду 
решается подстановкой:
Пример 19 Решить Решение: Данное уравнение является однородным, т.е. функции
разделяя переменные, получим:
Так как у нас
Линейные дифференциальные уравнения Уравнение где Неизвестная функция Линейные уравнения обычно решают методом Бернулли. Представим искомую функцию в виде произведения двух неизвестных функций Пусть и уравнение примет вид
Полученное уравнение разобьём на два таким образом: 1) Выберем функцию
2) Решаем первое: так как
Функцию
Найдём общее решение по формуле
подставив найденные функции вместо Пример 20 Решить уравнение Решение: Положим Подставляя выражения для
1) 2) Решаем первое уравнение: После разделения переменных получим Решаем второе уравнение: Подставим найденное значение
Отсюда, разделяя переменные и интегрируя, находим функцию
Теперь можно записать общее решение данного дифференциального уравнения:
Уравнением Бернулли называется уравнение вида
где Если Уравнение Бернулли можно сразу решать методом Бернулли, полагая
Пример 21 Решить уравнение Решение: Приведём решение методом Бернулли. Полагая
получим 1) 2) Подставим найденную функцию
и окончательно
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 218. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. .
. .
.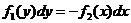 .
.
 .
. на
на  и умножим на
и умножим на  , получим уравнение с разделёнными переменными
, получим уравнение с разделёнными переменными
 , получим также уравнение с разделёнными переменными
, получим также уравнение с разделёнными переменными .
.
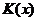 называется разделением переменных.
называется разделением переменных.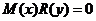 .
. , следует проверить, является ли оно решением исходного уравнения. Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл. Если входит, то оно есть частное решение, а если не входит, то это решение называется особым.
, следует проверить, является ли оно решением исходного уравнения. Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл. Если входит, то оно есть частное решение, а если не входит, то это решение называется особым.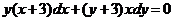 .
. , получим:
, получим: .
.

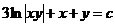 .
.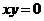 . Его решение
. Его решение 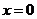 ,
,  является решением исходного уравнения, но не входит в общий интеграл. Следовательно, решение
является решением исходного уравнения, но не входит в общий интеграл. Следовательно, решение  .
.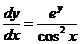 ;
; ;
; или
или 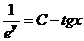 ;
; ;
; ;
;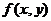 называется однородной степени
называется однородной степени  , если для любых
, если для любых  и
и  выполняется равенство
выполняется равенство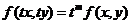
 и
и  однородные одной и той же степени
однородные одной и той же степени  называется однородным.
называется однородным. ,
, или
или  ;
;  .
. .
.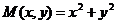 ,
,  однородные степени
однородные степени  . Сделаем замену Тогда уравнение перепишется так:
. Сделаем замену Тогда уравнение перепишется так: ;
; ;
; ;
;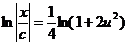 ;
; ;
;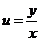 , то
, то  ,
,  ,
,  .
. ,
,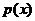 ,
, 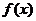 - непрерывная функция от
- непрерывная функция от  на интервале
на интервале  , называется линейным дифференциальным уравнением первого порядка.
, называется линейным дифференциальным уравнением первого порядка. и её производная входят в это уравнение в первой степени – линейно.
и её производная входят в это уравнение в первой степени – линейно.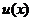 и
и  .
. , тогда
, тогда  или
или  ,
, или
или 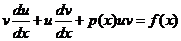 .
. ;
;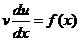 .
. , относительно
, относительно  с разделяющимися переменными:
с разделяющимися переменными: или
или 

 подставим во второе уравнение:
подставим во второе уравнение: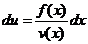 .
. .
. ,
,  .
. и
и  в данное уравнение получим:
в данное уравнение получим:
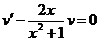
 .
. . Отсюда
. Отсюда  или
или  .
. .
.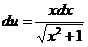
 .
. .
. ,
, – любое вещественное число.
– любое вещественное число. . Следует отметить, что при
. Следует отметить, что при  функция
функция  является решением Бернулли.
является решением Бернулли. .
. ;
; ;
; ;
; 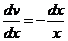 ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  ;
; 
 .
.