Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисления площадей плоских фигур
Пусть функция f(x) непрерывна на отрезке
Замечания: 1. Если же
или
Наконец, если линия y=f(x) пересекает ось Ох, то отрезок
2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле:
3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле:
Пример 11. Найти площадь плоской фигуры, ограниченной графиком функции y = sinx и осью абсцисс при условии Решение: Разобьём отрезок
Вычисление объёмов Если тело образовано вращением вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой y=f(x) (
Вокруг Оу:
Решение:
Несобственные интегралы При введении понятия определённого интеграла мы предполагали, что подынтегральная функция является ограниченной, а пределы интегрирования – конечными. Такой интеграл называется собственным (слово «собственный» обычно опускается). Если хотя бы одно из этих двух условий не выполнено, то интеграл называется несобственным.  Интегралы с бесконечными пределами интегрирования Пусть функция f(x) непрерывна при
Если этот предел существует, то говорят, что интеграл
сходится, а если предел не существует, то интеграл называют расходящимся. Геометрически для неотрицательной при
Пример 13 Исследовать на сходимость интегралы: а) б) в) Установим, при каких значениях Случай
Значит, данный интеграл сходится при Аналогично определяются следующие несобственные интегралы
|
||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 217. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
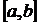 . Если при этом f(x)
. Если при этом f(x)  на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:

 на
на 





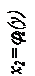
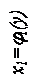

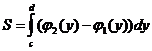
 .
. на два отрезка:
на два отрезка: 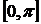 и
и  . На первом из них sinx
. На первом из них sinx  . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь:

 ), осью Ох и прямыми x=a, x=b (a<b), то
), осью Ох и прямыми x=a, x=b (a<b), то
 или
или 


 Пример 12 Найти объем тела, полученного вращением y=tgx вокруг оси Ox,
Пример 12 Найти объем тела, полученного вращением y=tgx вокруг оси Ox,  .
. .
. <
<  , т.е. при
, т.е. при  Тогда по определению полагают
Тогда по определению полагают

 функции f(x) несобственный интеграл по аналогии с собственным интегралом представляет собой площадь фигуры, ограниченной сверху графиком функции y=f(x), слева отрезком прямой x=a и снизу осью Ox.
функции f(x) несобственный интеграл по аналогии с собственным интегралом представляет собой площадь фигуры, ограниченной сверху графиком функции y=f(x), слева отрезком прямой x=a и снизу осью Ox.
 т.е. данный несобственный интеграл сходится.
т.е. данный несобственный интеграл сходится. т.е. данный интеграл расходится.
т.е. данный интеграл расходится. интеграл
интеграл  сходится.
сходится. был рассмотрен в примере б). Если
был рассмотрен в примере б). Если  то
то .
.