
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегралы от неограниченных функцийПусть функция f(x) непрерывна при
Если этот предел существует, то говорят, что интеграл
сходится, а если предел не существует, то интеграл называют расходящимся. Подобным же образом равенство
даёт определение интеграла от функции f(x), стремящейся к бесконечности при Наконец, если функция f(x) стремится к бесконечности при приближении аргумента к обоим концам промежутка
Если при этом сходятся оба интеграла в правой части последнего равенства, то сходится и интеграл слева. Пример 14
Понятие двойного интеграла Рассмотрим функцию двух переменных z=f(x,y) или z=f(M), определённую и непрерывную в замкнутой ограниченной области D плоскости Oxy;
Разобьем область D произвольным образом на элементарные участки Интегральной суммой для функции по области называется:
Если существует предел последовательности интегральных сумм
Замечание: Предел не зависит ни от способа разбиения области на элементарные участки Вычисление двойного интеграла сводится к вычислению повторных интегралов следующим образом.
Для непрерывной функции
или
Повторные интегралы (1) и (2) отличаются друг от друга порядком интегрирования по переменным 
Формулу (2) применяют в тех случаях, когда область
Вычисление двойного интеграла в декартовой системе координат сводится к последовательному вычислению двух определенных интегралов по формулам (1) или (2). При применении формулы (1) сначала вычисляют внутренний интеграл Если применяют формулу (2), то сначала вычисляют внутренний интеграл Покажем, как вычисляется двойной интеграл в декартовой системе координат. Пример 15 Вычислить Решение: Построим область
Найдем координаты точек пересечения параболы и прямой, для этого решим систему уравнений:
Решая второе уравнение, найдем
Вычисляя сначала внутренний интеграл по dx , затем внешний, получим:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ |
|||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 229. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 <b. Пусть эта функция стремится к бесконечности, когда
<b. Пусть эта функция стремится к бесконечности, когда 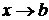 (т.е. на отрезке
(т.е. на отрезке 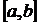 функция f(x) не ограничена). Положим
функция f(x) не ограничена). Положим

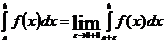
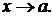
 , то полагают
, то полагают a<c<b.
a<c<b. , т.е. расходится.
, т.е. расходится. .
.
 , площади которых также обозначим
, площади которых также обозначим  , а диаметры
, а диаметры  .
. .
. при
при 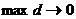 , то он называется двойным интегралом от функции f(M) по области D, обозначают:
, то он называется двойным интегралом от функции f(M) по области D, обозначают:
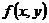 двойной интеграл по области
двойной интеграл по области  равен повторному интегралу:
равен повторному интегралу: (1)
(1)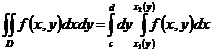 (2)
(2) и
и  . Применение формулы (1) или (2) зависит от конфигурации области
. Применение формулы (1) или (2) зависит от конфигурации области 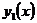 и
и  , а слева и справа прямыми
, а слева и справа прямыми  , причем всюду на
, причем всюду на 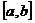 функции
функции 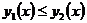 . Примеры таких областей приведены на рисунке.
. Примеры таких областей приведены на рисунке.
 и
и  . Снизу и сверху - прямыми
. Снизу и сверху - прямыми  . Причем всюду на
. Причем всюду на 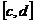 функции
функции  непрерывны
непрерывны  . На рисунке изображены примеры таких областей.
. На рисунке изображены примеры таких областей.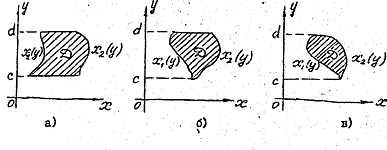
 при постоянном
при постоянном  до
до  .
. при постоянном
при постоянном  где область
где область  .
. является уравнением параболы, симметричной относительно оси
является уравнением параболы, симметричной относительно оси 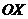 , с вершиной в начале координат. Уравнение
, с вершиной в начале координат. Уравнение  есть уравнение прямой.
есть уравнение прямой.

 - ординаты точек пересечения параболы и прямой. Таким образом, область
- ординаты точек пересечения параболы и прямой. Таким образом, область  , справа прямой
, справа прямой  , снизу н сверху соответственно прямыми
, снизу н сверху соответственно прямыми  и
и 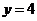 . Применяя формулу (2), запишем исходный двойной интеграл в виде
. Применяя формулу (2), запишем исходный двойной интеграл в виде ,
,