
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обыкновенные дифференциальные уравненияŸ Дифференциальные уравнения первого порядка. Задача Коши. Ÿ Теорема существования и единственности решения задачи Коши. Ÿ Частное, общее и особое решения дифференциального уравнения. Ÿ Основные типы уравнений первого порядка : уравнения с разделяющимися переменными, однородные, линейные, , уравнения Бернулли. Ÿ Дифференциальные уравнения второго порядка. Задача Коши. Ÿ Теорема существования и единственности решения задачи Коши. Ÿ Уравнения, допускающие понижение порядка. Ÿ Линейные дифференциальные уравнения второго порядка: Ÿ однородные и неоднородные. Структура общего решения. Ÿ Однородные линейные дифференциальные уравнения с Ÿ постоянными коэффициентами. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида. Ÿ Метод Лагранжа вариации произвольных постоянных. Ÿ Приложения дифференциальных уравнений в экономике.
Теория рядов. Ÿ Сходимость и сумма числового ряда. Необходимое условие сходимости числового ряда. Достаточные признаки сходимости числовых рядов с положительными членами. Ÿ Знакопеременные ряды. Теорема Лейбница. Ÿ Функциональные ряды Степенные ряды. Разложение функции в степенной ряд. Ряды Тейлора, Маклорена.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 2.1 Неопределённый интеграл, его свойства Первообразная функция и неопределённый интеграл Функция F(x) называется первообразной функцией для данной функции f(x) на данном промежутке, если на этом промежутке
Например, функция F(x)=x3 является первообразной функции f(x)=3x2 на всей числовой оси, так как (x3)/=3x2 при любом x. Отметим, что вместе с функцией F(x)=x3 первообразной для f(x)=3x2 является любая функция вида Ф(х)=х3+С, где С – произвольное постоянное число.  Лемма о первообразных Если F1(x) и F2(x) – две первообразные для функции f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу. Из этой теоремы следует, что если известна какая-нибудь первообразная F(x) данной функции f(x), то всё множество первообразных для f(x) можно записать в виде F(x)+C. Выражение F(x)+C, где F(x) – первообразная функции f(x) и С – произвольная постоянная, называется неопределённым интегралом от функции f(x) и обозначается символом х– переменной интегрирования; Таким образом, по определению
если Возникает вопрос: для всякой ли функции f(x) существует первообразная, а значит, и неопределённый интеграл?
Свойства неопределённого интеграла 1. Производная от неопределенного интеграла равна подынтегральной функции
2. Дифференциал неопределенного интеграла равен подынтегральному выражению
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого
где С – произвольное число 4. Постоянный множитель можно выносить за знак интеграла
где k – некоторое число. 5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций
Интегралы от основных элементарных функций (Таблица интегралов) 1) 2) 3) 4) 5) 6) 7) 8)
Методы интегрирования
Пример 1. Найти интеграл Решение:
Пример 2. Найти интеграл Решение:
Если
Пример 3. Найти интеграл Решение: Воспользуемся подстановкой x=t2. Тогда
Пусть u=u(x) и v=v(x) – непрерывно дифференцируемые функции. Тогда справедлива формула
Пример 4. Найти интеграл Решение: Пусть u=x
Многочленом степени n называется выражение вида
Рациональной дробью называется отношение двух многочленов. Например, где Простейшими рациональными дробями являются следующие четыре типа дробей: I) Очевидно, что интегралы от простейших дробей первого и второго типов находятся легко: где k – целое, От дробей третьего и четвёртого типов вычисляют заменой
Для любых многочленов Если z - корень комплексный: и Любой многочлен можно разложить на линейные и квадратичные множители Правильную рациональную дробь можно разложить на сумму простейших дробей, если знаменатель дроби
Пример 5. Разложить на сумму простейших дробей следующие дроби: а) б) Решение: а) б)
Пример 6. Вычислить интеграл:
Решение: Разложим подынтегральную дробь на простейшие дроби
приравнивая числители дробей, получаем:
Определим коэффициенты А и В, придавая любые значения переменной x:
Получаем А=1 и В=1. Исходный интеграл найдём как сумму интегралов от полученных дробей.
Такая замена называется универсальной тригонометрическая подстановкой. В этом случае,
Тогда
Пример 7. Найти Решение: Положим
рассмотрим частные случаи: n – нечётное
n, m – чётные,
применяют формулы тригонометрии:
где n, m – чётные, применяют формулу:
Пример 8. Вычислить интегралы: а) б) Решение: а) б)
используют формулы
При вычислении интегралов, содержащих иррациональные выражения применяют замену переменной. Если то
Если то |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 192. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ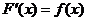 .
.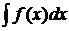 , причём f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением,
, причём f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением,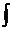 – знак неопределённого интеграла.
– знак неопределённого интеграла.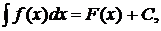
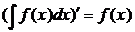

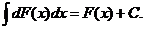 или
или 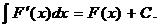
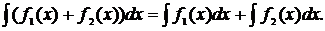

 .
. , в общем случае
, в общем случае 
 , в частности
, в частности 
 9)
9) 
 10)
10) 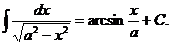
 11)
11) 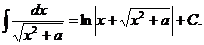
 12)
12) 
 Метод непосредственного интегрирования связан с приведением подынтегрального выражения к табличной форме путём преобразований и применения свойств неопределённого интеграла.
Метод непосредственного интегрирования связан с приведением подынтегрального выражения к табличной форме путём преобразований и применения свойств неопределённого интеграла.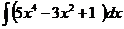
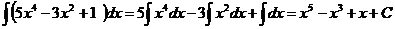 .
.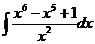
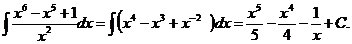
 , где
, где 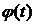 - функция, имеющая непрерывную производную, тогда
- функция, имеющая непрерывную производную, тогда 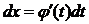 ; подставляя в интеграл, получим
; подставляя в интеграл, получим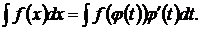

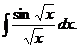
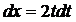 , получим
, получим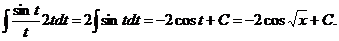
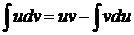 .
.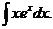
 du=dx,
du=dx,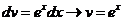 ; Используя формулу интегрирования по частям, получим
; Используя формулу интегрирования по частям, получим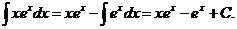
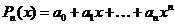 , где
, где 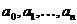 – действительные числа
– действительные числа 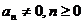 . Например, 5–7x – многочлен первой степени
. Например, 5–7x – многочлен первой степени 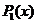 ,
,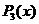 =2x3 – 3x2 +8x – 1 – многочлен третьей степени.
=2x3 – 3x2 +8x – 1 – многочлен третьей степени.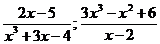 – рациональные дроби. Всякая рациональная дробь имеет вид:
– рациональные дроби. Всякая рациональная дробь имеет вид:
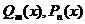 – многочлены степени m и n соответственно.
– многочлены степени m и n соответственно.


 ; II)
; II)  III)
III)  ; IV)
; IV) 
 ,
,
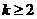 .
. , или по следующим формулам:
, или по следующим формулам: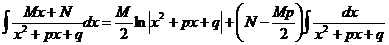

 имеет место теорема Безу:
имеет место теорема Безу: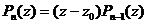 , где z0 - простой корень
, где z0 - простой корень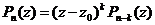 , где z0 - корень кратности k.
, где z0 - корень кратности k.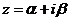 , где i=
, где i= 
 , то
, то  , где
, где  – сопряженный корень.
– сопряженный корень.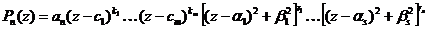

 – действительные корни;
– действительные корни;  - комплексные корни
- комплексные корни представлен в виде сомножителей
представлен в виде сомножителей 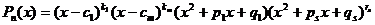 :
:
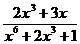 ;
;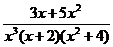 .
.
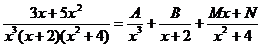
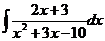
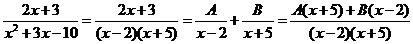
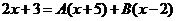
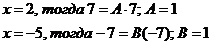

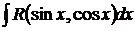 . Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной
. Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной 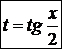 , где
, где 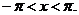
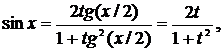
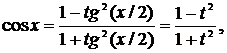
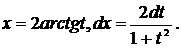
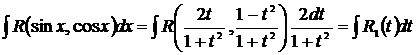 .
.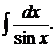
 . Тогда, используя выражения через t для dx и sinx, указанные выше, получаем, что искомый интеграл равен
. Тогда, используя выражения через t для dx и sinx, указанные выше, получаем, что искомый интеграл равен

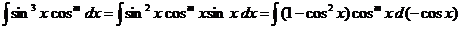
 .
.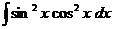


 делают замену
делают замену  , тогда
, тогда


 ,
,

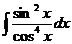




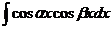



 ,
,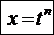 , где
, где 
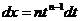

 , где
, где 