
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Властивості абсолютно й умовно збіжних рядівТеорема. Якщо ряд збігається абсолютно, то він залишається абсолютно збіжним при будь-якій перестановці його членів. При цьому сума ряду не залежить від порядку його членів. Теорема. Якщо ряд збігається умовно, то яке б ми ні задали число А, можна так переставити члени цього ряду, щоб його сума виявилася в точності рівною А. Більш того, можна так переставити члени умовно збіжного ряду, щоб ряд, отриманий після перестановки, виявився розбіжним. Приклад. Знакозмінний ряд
Далі,
Таким чином,
ФУНКЦІОНАЛЬНІ РЯДИ ЛЕКЦІЯ 24. ОБЛАСТЬ ЗБІЖНОСТІ ФУНКЦІОНАЛЬНОГО РЯДУ 24.1. Область збіжності функціонального ряду Означення. Ряд
Даючи х визначені числові значення, ми одержуємо різні числові ряди, які можуть виявитися збіжними або розбіжними. Означення. Сукупність тих значень х, при яких функціональний ряд збігається, називають областю збіжності цього ряду. Очевидно, що в області збіжності ряду його сума є деяка функція від х. Тому суму функціонального ряду позначають через  Представимо суму ряду у вигляді
[ Для всіх значень х в області збіжності ряду має місце співвідношення
ЛЕКЦІЯ 25. СТЕПЕНЕВИЙ РЯД, ЙОГО ОБЛАСТЬ ТА ІНТЕРВАЛ ЗБІЖНОСТІ. ВЛАСТИВОСТІ СТЕПЕНЕВИХ РЯДІВ. РАДІУС ЗБІЖНОСТІ СТЕПЕНЕВОГО РЯДУ |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 294. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
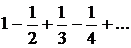 (23.3) збігається умовно. Позначимо його суму через S. Очевидно, що
(23.3) збігається умовно. Позначимо його суму через S. Очевидно, що  . Зробимо перестановку членів ряду так, щоб за одним додатним членом ішли два від'ємних:
. Зробимо перестановку членів ряду так, щоб за одним додатним членом ішли два від'ємних: (23.4)
(23.4) в два рази менше суми вихідного ряду, тобто
в два рази менше суми вихідного ряду, тобто  . Позначимо через
. Позначимо через  і
і  часткові суми рядів (23.3) і (23.4). Розглянемо суму
часткові суми рядів (23.3) і (23.4). Розглянемо суму  членів ряду (23.4):
членів ряду (23.4):
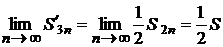 .
. .
. .
.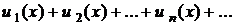 ,
,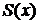 .
. , де
, де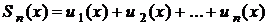 ,
, 
 - залишок функціонального ряду].
- залишок функціонального ряду]. , тому
, тому ,
,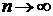 .
.