
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Гранична форма ознаки порівнянняГранична форма ознаки порівняння. Якщо Приклад. Дослідити на збіжність ряд Розв'язок. Порівняємо ряд із гармонічним рядом
Отже, даний ряд розбігається. Ознака Даламбера Ознака Даламбера. Нехай маємо ряд із додатними членами Приклад. Дослідити на збіжність ряд Розв'язок. Скористаємося ознакою Даламбера; маємо
Даний ряд збігається. Радикальна ознака Коші Радикальна ознака Коші. Якщо для ряду з невід'ємними членами Приклад. Дослідити на збіжність ряд Розв'язок. Тут зручно застосувати ознаку Коші, оскільки
Даний ряд збігається. Інтегральна ознака Коші Інтегральна ознака Коші. Нехай дано ряд
Приклад. Дослідити на збіжність ряд Розв'язок. Скористуємося інтегральною ознакою Коші:
ЛЕКЦІЯ 23. ЗНАКОЗМІННІ РЯДИ. АБСОЛЮТНА І УМОВНА ЗБІЖНІСТЬ. РЯДИ ЗІ ЗНАКОЧЕРГУВАННЯМ. ОЗНАКА ЛЕЙБНІЦА. ВЛАСТИВОСТІ ЗНАКОЗБІЖНИХ РЯДІВ  23.1. Знакозмінні ряди. Теорема Лейбніца Будемо розглядати ряди, члени яких мають знакозмінні знаки, тобто ряди виду
Теорема Лейбніца. Якщо у знакозмінному ряді члени такі, що Зауваження. Теорема Лейбніца справедлива, якщо нерівності Приклад. Дослідити на збіжність ряд Розв'язок. Застосуємо теорему Лейбніца. Тому що Знакопереміжні ряди. Абсолютна й умовна збіжність Означення. Знакозмінний ряд Приклад. Дослідити на збіжність ряд Розв'язок. Перша умова ознаки Лейбніца виконується: Складемо ряд з абсолютних величин: Приклад. Дослідити на збіжність ряд Розв'язок. Перша умова ознаки Лейбніца виконується: Складемо ряд з абсолютних величин:
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 411. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 і
і  - ряди з невід'ємними членами й існує кінцевий, відмінний від нуля
- ряди з невід'ємними членами й існує кінцевий, відмінний від нуля  , то розглянуті ряди одночасно збігаються або розбігаються.
, то розглянуті ряди одночасно збігаються або розбігаються.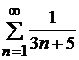 .
. .
. .
. , то при
, то при  ряд збігається, при
ряд збігається, при  ряд розбігається, при
ряд розбігається, при  потрібні додаткові дослідження - ознака відповіді не дає.
потрібні додаткові дослідження - ознака відповіді не дає. .
. ,
,  ; виходить,
; виходить, .
. існує
існує  , то при
, то при 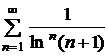 .
.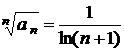 , а границя останнього дробу знаходиться просто:
, а границя останнього дробу знаходиться просто: .
. при цілих значеннях аргументу х:
при цілих значеннях аргументу х: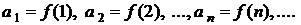
 . Тоді ряд збігається, якщо збігається невласний інтеграл
. Тоді ряд збігається, якщо збігається невласний інтеграл  , і розбігається, якщо цей інтеграл розбігається.
, і розбігається, якщо цей інтеграл розбігається.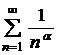 .
. ; отже,
; отже,  .
. При
При  :
:  . Ряд розбігається.
. Ряд розбігається. .
.
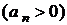
 і
і 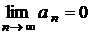 , то ряд збігається, його сума додатна і не перевершує першого члена.
, то ряд збігається, його сума додатна і не перевершує першого члена. виконуються, починаючи з деякого N.
виконуються, починаючи з деякого N.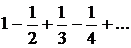
 , то перша умова теореми виконується. Далі, тому що
, то перша умова теореми виконується. Далі, тому що  , то виконана і друга умова. Виходить, даний ряд збігається.
, то виконана і друга умова. Виходить, даний ряд збігається.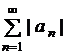 . Якщо ж знакозмінний ряд
. Якщо ж знакозмінний ряд  .
. , то виконана і друга умова. Виходить, даний ряд збігається.
, то виконана і друга умова. Виходить, даний ряд збігається. . Даний гармонічний ряд розбігається, отже, знакозмінний ряд збігається умовно.
. Даний гармонічний ряд розбігається, отже, знакозмінний ряд збігається умовно. .
. Тому що
Тому що  , то виконана і друга умова. Виходить, даний ряд збігається.
, то виконана і друга умова. Виходить, даний ряд збігається.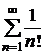 . Дослідимо збіжність даного ряду, використовуючи ознаку Даламбера; маємо:
. Дослідимо збіжність даного ряду, використовуючи ознаку Даламбера; маємо: 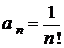 ,
,  .
. ,
,