
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод Лагранжа (метод варіації довільної сталої) для розв'язку лінійних рівнянь першого порядкуСуть методу полягає в тому, що спочатку знаходимо загальний розв'язок відповідного лінійного однорідного рівняння
Він співпадає з розв'язком (17.6). Приклад. Розв'язати рівняння методом Лагранжа
Розв'язок. Розв'яжемо відповідне однорідне рівняння
Вважаючи в цьому розв'язку сталу С функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:
Підставимо у вихідне рівняння у,
Тому що
ЛЕКЦІЯ 18. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ВИШИХ ПОРЯДКІВ. РІВНЯННЯ, ЯКІ ДОПУСКАЮТЬ ЗНИЖЕННЯ ПОРЯДКУ. ЗАДАЧА КОШІ 18.1. Рівняння виду Розв'язок цього рівняння знаходиться n-кратним інтегруванням:
…………………………………………………
Тому що
Приклад. Знайти розв'язок задачі Коші: Розв'язок. Знайдемо загальний розв'язок послідовним інтегруванням даного рівняння
Скористаємося початковими умовами:
Отже, шуканий частинний розв'язок має вигляд:
Рівняння II порядку, що дозволяють зниження порядку Випадок 1.  Приклад. Розв'язати рівняння Розв'язок. Це рівняння не містить у. Вважаючи Інтегруємо його. Вважаючи в рівнянні
Визначаємо Визначимо
Повертаючись до змінної у, маємо
Випадок 2. Диференціальне рівняння виду Рівняння цього виду допускає зниження порядку за допомогою заміни Приклад. Розв'язати рівняння Розв'язок. Вважаючи
Розділимо змінні і проінтегруємо:
Повертаючись до змінної
ЛЕКЦІЯ 19. ЛІНІЙНІ ОДНОРІДНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ДРУГОГО ПОРЯДКУ ІЗ СТАЛИМИ КОЕФІЦІЕНТАМИ. ЛІНІЙНІ НЕОДНОРІДНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ДРУГОГО ПОРЯДКУ ІЗ СТАЛИМИ КОЕФІЦІЕНТАМИ ЗІ СПЕЦІАЛЬНОЮ ПРАВОЮ ЧАСТИНОЮ 19.1. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами Означення. Рівняння виду Теорема. Якщо Для визначення частинних розв'язків
У залежності від коренів характеристичного рівняння загальний розв'язок шукаємо у вигляді: а) якщо корені рівняння б) якщо корені рівняння в) якщо корені рівняння Приклад. Знайти загальний розв'язок рівняння Розв'язок. Складемо характеристичне рівняння
Приклад. Знайти розв'язок задачі Коші: Розв'язок. Складемо характеристичне рівняння
Підставляючи початкові умови в загальний розв'язок і його похідну, одержимо систему рівнянь відносно
Виходить, розв'язок, який задовольняє поставленим початковим умовам, має вигляд:
Приклад. Знайти загальний розв'язок рівняння Розв'язок. Складемо характеристичне рівняння
19.2. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами Розглянемо тепер неоднорідне рівняння
Означення. Якщо в (19.1) Теорема 1. Якщо відомий який-небудь частинний розв'язок Доказ. Потрібно довести, що сума Доведемо спочатку, що функція Підставляючи суму
Тому що у є розв'язок рівняння Доведемо тепер, що вираз
Помітивши, що у можна представити у формі
Тоді на підставі умов
З цієї системи рівнянь потрібно визначити
зауважуємо, що визначник цієї системи є визначник Вронського для функцій Теорема 2. Якщо Доказ. Складаючи ліві і праві частини рівностей
Теореми, за допомогою яких знаходяться частинні розв'язки лінійних неоднорідних диференціальних рівнянь для спеціальних правих частин: Теорема 3. Якщо права частина лінійного диференціального рівняння із сталими коефіцієнтами має вид
Зокрема, при Теорема 4. Якщо ж права частина лінійного диференціального рівняння із сталими коефіцієнтами може бути подана у вигляді
і многочлени степені n. Якщо ж
Приклад. Вирішити рівняння Розв'язок. Вирішимо відповідне однорідне рівняння Тому що права частина даного неоднорідного рівняння має вид
Підставимо цей вираз в задане рівняння
Прирівнюючи коефіцієнти при однакових степенях х, получимо
Відкіля
Приклад. Знайти загальний розв'язок рівняння Розв'язок. Вирішимо відповідне однорідне рівняння Тут права частина має вид
Підставляючи
Прирівнюючи коефіцієнти при однакових степенях х, получимо
Приклад. Знайти загальний інтеграл лінійного неоднорідного рівняння Розв'язок. Характеристичне рівняння
Частинний розв'язок неоднорідного рівняння шукаємо у виді
Підставляючи
Прирівнюючи коефіцієнти при
Приклад. Вирішити рівняння Розв'язок. Характеристичне рівняння має корені
Частинний розв'язок неоднорідного рівняння шукаємо у формі
Тоді
Підставляючи ці вирази похідних у дане рівняння і прирівнюючи коефіцієнти при
Таким чином, загальний інтеграл даного рівняння
ЧИСЛОВІ РЯДИ |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 554. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

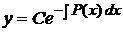 .
. . (17.7)
. (17.7) ,
,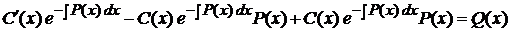 ,
, ,
, 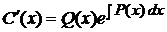 ,
,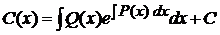 ,
, . (17.8)
. (17.8) .
.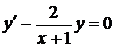 ,
,  ,
, 
 ,
,  .
. ,
, 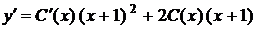 .
.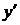 і з отриманого диференціального рівняння знайдемо функцію
і з отриманого диференціального рівняння знайдемо функцію 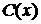 :
: ,
, ,
,  .
. - загальний розв'язок.
- загальний розв'язок. , то
, то 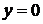 - теж розв'язок вихідного рівняння.
- теж розв'язок вихідного рівняння.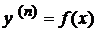
 ,
, ,
, ,
,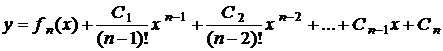 ,
, .
. , є сталі, то загальний розв'язок може бути записаний і так:
, є сталі, то загальний розв'язок може бути записаний і так: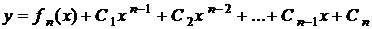 .
.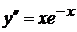 ,
,  .
. ,
, .
. .
.
 :
: 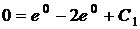 ,
,  .
.  :
:  ,
,  .
. .
. . Заміна
. Заміна  ,
,  .
. .
. .
. ,
, 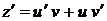 , одержимо:
, одержимо: ,
,  .
. , поклавши
, поклавши  ,
,  ,
,  , відкіля
, відкіля  , або
, або  .
. :
: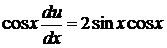 ,
,  , відкіля
, відкіля  ; отже,
; отже, .
.

 ,
, ,
, .
.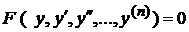 , яке не містить незалежної змінної.
, яке не містить незалежної змінної. , або
, або  .
. .
. , отримаємо рівняння I порядку відносно невідомих
, отримаємо рівняння I порядку відносно невідомих 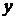 і
і  .
. .
. ,
,  ,
,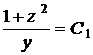 ,
,  ,
,  .
.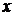 , отримаємо
, отримаємо ,
, 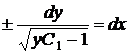 ,
, 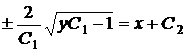 ,
, ,
,  ,
,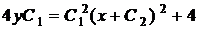 ,
,  .
.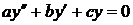 , де a, b, c - сталі, називається лінійним однорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами.
, де a, b, c - сталі, називається лінійним однорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами.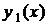 і
і  - два лінійно-незалежні частинні розв'язки рівняння
- два лінійно-незалежні частинні розв'язки рівняння  , то загальний розв'язок цього рівняння
, то загальний розв'язок цього рівняння  .
. ,
, ,
,  .
. - дійсні різні, то загальний розв'язок
- дійсні різні, то загальний розв'язок  ;
; - дійсні рівні, то загальний розв'язок
- дійсні рівні, то загальний розв'язок  ;
; - комплексні спряжені, то загальний розв'язок
- комплексні спряжені, то загальний розв'язок  .
. .
. ; його корені
; його корені  ,
, 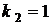 . Отже, загальний розв'язок має вигляд:
. Отже, загальний розв'язок має вигляд: .
.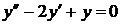 ,
,  ,
,  .
.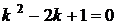 ; його корені
; його корені  . Отже, загальний розв'язок має вигляд:
. Отже, загальний розв'язок має вигляд: .
. і
і  .
.


 .
. .
. ; його корені
; його корені  . Корені характеристичного рівняння комплексні сполучені, а тому загальний розв'язок є
. Корені характеристичного рівняння комплексні сполучені, а тому загальний розв'язок є .
. , (19.1)
, (19.1) і з неперервною правою частиною
і з неперервною правою частиною  .
. , то рівняння
, то рівняння  називається відповідним однорідним рівнянням.
називається відповідним однорідним рівнянням. неоднорідного рівняння
неоднорідного рівняння 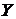 є сума цього частинного розв'язку і загального розв'язку у відповідного однорідного рівняння
є сума цього частинного розв'язку і загального розв'язку у відповідного однорідного рівняння 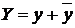 .
. в рівняння
в рівняння  ,
,  .
. ,
, (аби
(аби  було узято з тієї області, де функція
було узято з тієї області, де функція  ,
, і
і  - лінійно незалежні розв'язки рівняння
- лінійно незалежні розв'язки рівняння  .
. ,
,  .
.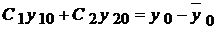 ,
,  ,
,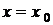 . Тому що ці функції за умовою лінійно незалежні, то визначник Вронського не дорівнює нулю; отже, система має визначений розв'язок
. Тому що ці функції за умовою лінійно незалежні, то визначник Вронського не дорівнює нулю; отже, система має визначений розв'язок 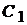 і
і  , при яких формула
, при яких формула  , а
, а 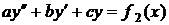 , то
, то  - частинний розв'язок рівняння
- частинний розв'язок рівняння  .
. і
і  , получимо
, получимо .
.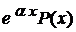 , де
, де  - многочлен n-ої степені і
- многочлен n-ої степені і 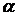 не є коренем характеристичного рівняння, то існує частинний розв'язок вигляду
не є коренем характеристичного рівняння, то існує частинний розв'язок вигляду  , де
, де  - деякий многочлен n-ої степені:
- деякий многочлен n-ої степені: .
. або
або 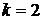 ), то існує частинний розв'язок вигляду
), то існує частинний розв'язок вигляду  .
. права частина - многочлен n-ої степені, і якщо
права частина - многочлен n-ої степені, і якщо  .
. ,
, і
і  - многочлени (n - найбільша з їх степенів) і
- многочлени (n - найбільша з їх степенів) і  не є коренем характеристичного рівняння, то існує частинний розв'язок виду
не є коренем характеристичного рівняння, то існує частинний розв'язок виду ,
, -
- .
. .
. . Складемо характеристичне рівняння
. Складемо характеристичне рівняння 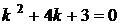 ; його корені
; його корені  ,
,  . Загальний розв'язок відповідного однорідного рівняння є
. Загальний розв'язок відповідного однорідного рівняння є 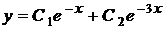 .
. (тобто вид
(тобто вид  ), причому 0 не є коренем характеристичного рівняння
), причому 0 не є коренем характеристичного рівняння  .
. ,
, 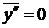 .
. ,
,  .
.

 ,
,  . Отже,
. Отже,  . Загальний розв'язок
. Загальний розв'язок  .
. .
. . Складемо характеристичне рівняння
. Складемо характеристичне рівняння  , причому коефіцієнт 1 у показнику степені є простим коренем характеристичного многочлена. Отже, частинний розв'язок шукаємо у виді
, причому коефіцієнт 1 у показнику степені є простим коренем характеристичного многочлена. Отже, частинний розв'язок шукаємо у виді ,
, 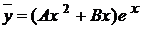
 ,
, .
. в задане рівняння, будемо мати
в задане рівняння, будемо мати
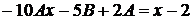 .
. ,
,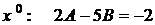 ,
, ,
,  . Отже, частинним розв'язком є
. Отже, частинним розв'язком є ,
, .
. .
. має корені
має корені  ;
;  . Тому загальний інтеграл відповідного однорідного рівняння є
. Тому загальний інтеграл відповідного однорідного рівняння є .
.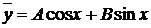 ,
,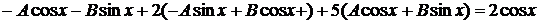 .
. і
і 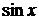 , одержимо систему двох рівнянь для визначення А і В:
, одержимо систему двох рівнянь для визначення А і В:
 ,
,  . Загальний розв'язок даного рівняння
. Загальний розв'язок даного рівняння  .
. .
. ;
;  : тому загальний розв'язок однорідного рівняння має вид
: тому загальний розв'язок однорідного рівняння має вид .
. .
. ,
, .
.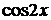 і
і  , одержуємо систему рівнянь для визначення А і В:
, одержуємо систему рівнянь для визначення А і В: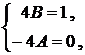
 ,
,  .
. .
.