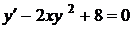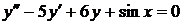Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Інтеграл від необмеженої функції(невласні інтеграли II роду) Нехай функція Інтеграл Означення. Якщо границя, яка стоїть справа, існує, то інтеграл називають невласним збіжним інтегралом, у противному випадку інтеграл називають розбіжним. Якщо функція Якщо функція Приклад. Обчислити невласні інтеграли: а)
б)
Отже, даний інтеграл розбігається. Зауваження. Якщо функція ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ЛЕКЦІЯ 15. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ, ОСНОВНІ ВИЗНАЧЕННЯ. ПОНЯТТЯ ЗАГАЛЬНОГО ТА ЧАСТИННОГО РОЗВ'ЯЗКУ. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ПЕРШОГО ПОРЯДКУ. РІВНЯННЯ З РОЗДІЛЕНИМИ ЗМІННИМИ ТА ЗМІННИМИ, ЯКІ РОЗДІЛЯЮТЬСЯ Диференціальні рівняння, основні визначення Означення. Звичайним диференціальним рівнянням називається рівняння, яке зв'язує незалежну змінну х, шукану функцію  Символічно диференціальне рівняння можна записати так:
Означення. Порядком диференціального рівняння називається порядок найвищої похідної, що входить у рівняння. Так, наприклад, рівняння
Рівняння
Означення. Розв'язком або загальним інтегралом диференціального рівняння називається така функція |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 275. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
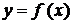 визначена і неперервна при
визначена і неперервна при 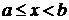 , а при
, а при 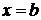 функція або не визначена, або терпить розрив. У цьому випадку не можна говорити про інтеграл
функція або не визначена, або терпить розрив. У цьому випадку не можна говорити про інтеграл 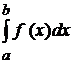 як про границю інтегральних сум, тому що
як про границю інтегральних сум, тому що 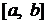 , і тому ця границя може і не існувати.
, і тому ця границя може і не існувати.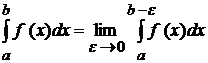 .
.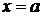 ), то по означенню
), то по означенню 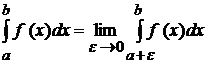 .
.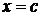 , яка лежить усередині відрізка
, яка лежить усередині відрізка 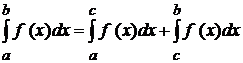 , якщо обидва невласних інтеграли, які стоять у правій частині рівності, існують.
, якщо обидва невласних інтеграли, які стоять у правій частині рівності, існують.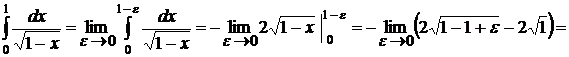
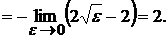
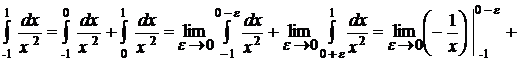
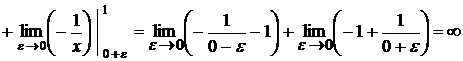 .
.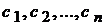 , то інтеграл від функції
, то інтеграл від функції 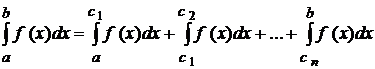 , якщо кожний із невласних інтегралів у правій частині рівності збігається. Якщо ж хоча б один із цих інтегралів розбігається, то і
, якщо кожний із невласних інтегралів у правій частині рівності збігається. Якщо ж хоча б один із цих інтегралів розбігається, то і 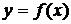 та її похідні
та її похідні 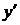 ,
, 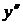 , …,
, …, 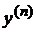 ,...
,...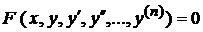
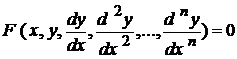 .
.