
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Диференціальні рівняння першого порядку (загальні поняття)Диференціальне рівняння першого порядку має вигляд
Якщо це рівняння можна розв'язати відносно
Для такого рівняння справедлива наступна теорема, яка називається теоремою існування і одиничності розв'язку диференціального рівняння. Теорема.Якщо в рівнянні Геометричний зміст теореми полягає в тому, що існує і притім єдина функція Означення. Умова, що при
Означення. Задача, у якій потрібно знайти частинний розв'язок рівняння Означення. Загальним розв'язком диференціального рівняння першого порядку називається функція
а) вона задовольняє диференціальному рівнянню при будь-якому конкретному значенні сталої С; б) яка б не була початкова умова У процесі знаходження загального розв'язку диференціального рівняння ми приходимо до співвідношення вигляду 
Означення. Рівність вигляду Означення. Частинним розв'язком називається будь-яка функція З геометричної точки зору загальний інтеграл являє собою сімейство кривих на координатній площині, яке залежить від однієї довільної сталої С. Ці криві називаються інтегральними кривими даного диференціального рівняння. Частинному інтегралу відповідає одна крива цього сімейства, яка проходить через деяку задану точку площини. Вирішити або проінтегрувати диференціальне рівняння - значить: а) знайти його загальний розв'язок або загальний інтеграл (якщо початкові умови не задані) або б) знайти той частинний розв'язок рівняння, який задовольняє заданим початковим умовам (якщо такі є). Означення. Особливим розв'язком називається такий розв'язок, у всіх точках якого умова одиничності не виконується, тобто в будь-якому околі кожної точки Особливі розв'язки не утворюються з загального розв'язку диференціального рівняння ні при яких значеннях довільної сталої С (у тому числі і при |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 273. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.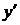 , то його можна записати у вигляді
, то його можна записати у вигляді .
.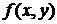 і її частинна похідна
і її частинна похідна  по у неперервні в деякій області D на площині 0ху, яка містить деяку точку
по у неперервні в деякій області D на площині 0ху, яка містить деяку точку  , то існує єдиний розв'язок цього рівняння
, то існує єдиний розв'язок цього рівняння 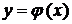 ,
,  при
при 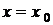 .
. , називається початковою умовою, або умовою Коши. Вона записується у вигляді
, називається початковою умовою, або умовою Коши. Вона записується у вигляді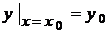 або
або  .
. ,
, , що функція
, що функція  задовольняє даній початковій умові. При цьому передбачається, що значення
задовольняє даній початковій умові. При цьому передбачається, що значення  і
і 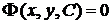 ,
, називається в цьому випадку частинним інтегралом рівняння.
називається в цьому випадку частинним інтегралом рівняння. особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.
особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.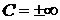 ).
).