
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Диференціальні рівняння із розділеними зміннимиОзначення. Диференціальне рівняння типу
Інтегруючи обидві частини цього рівняння, одержимо співвідношення, яке зв'язує розв'язок у, незалежну змінну х і довільну сталу С, тобто одержимо загальний інтеграл рівняння
Приклад. Знайти загальний розв'язок рівняння
Розв'язок.
Диференціальні рівняння із змінними, які розділяються Означення. Диференціальні рівняння, у яких змінні можна розділити за допомогою множення або ділення обох частин рівняння на той самий вираз, називаються диференціальними рівняннями із змінними, які розділяються. Це рівняння виду
Воно може бути приведене до рівняння із розділеними змінними шляхом ділення обох його частин на вираз
Приклад. Знайти загальний розв'язок рівняння
Розв'язок. Розділяючи змінні, знаходимо:
Інтегруючи, отримаємо:
Приклад. Розв'язати задачу Коші
Розв'язок. Розділяючи змінні, знаходимо:
Розв'язавши останнє рівняння відносно у, знайдемо загальний розв'язок вихідного рівняння
Знайдемо частинний розв'язок, який задовольняє початковій умові
ЛЕКЦІЯ 16. ОДНОРІДНІ РІВНЯННЯ, ЇХ РОЗВ'ЯЗОК. Однорідні рівняння першого порядку Означення. Функція 
Приклад.
Приклад.
Приклад.
Означення. Рівняння виду Однорідне рівняння зводиться до вигляду Приклад. Розв'язати задачу Коші
Розв'язок.
Знайдемо частинний розв'язок, який задовольняє початковій умові
ЛЕКЦІЯ 17. ЛІНІЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ПЕРШОГО ПОРЯДКУ. ПІДСТАНОВКА БЕРНУЛЛІ. МЕТОД ВАРІАЦІЇ ДОВІЛЬНОЇ СТАЛОЇ Лінійні рівняння першого порядку. Підстановка Бернуллі Означення. Лінійним рівнянням першого порядку називається рівняння, що має вигляд
Якщо Шукаємо розв'язок рівняння (17.1) у вигляді добутку двох функцій від х:
Підставши у і
Виберемо функцію
Так як нам досить якого-небудь відмінного від нуля розв'язку рівняння (17.5), то за функцію Підставляючи знайдене значення
Підставляючи
Розв'язок однорідного рівняння можна записати у вигляді:
Приклад. Розв'язати рівняння
Розв'язок. Скориставшись (17.2), (17.3)
Згідно методу виберемо функцію
Підставляючи
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 250. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

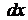 знаходиться тільки функція від х, а при
знаходиться тільки функція від х, а при 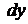 - тільки функція від у.
- тільки функція від у. .
. .
. ,
,  ,
, .
. .
.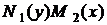 :
: ,
,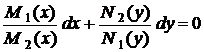 .
. .
. ,
,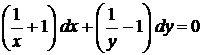 .
.
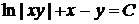 .
. ,
, 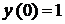 .
. .
.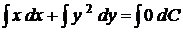 ,
,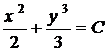 .
.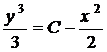 ,
, 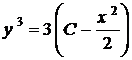 ,
,  .
. ,
,  ,
,  ,
, 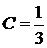 .
.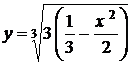 - розв'язок задачі Коші.
- розв'язок задачі Коші.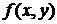 називається однорідною функцією n-го порядку щодо змінних х і у, якщо при будь-якому t справедлива тотожність
називається однорідною функцією n-го порядку щодо змінних х і у, якщо при будь-якому t справедлива тотожність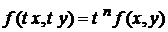 .
.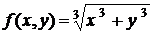 - однорідна функція першого порядку, тому що
- однорідна функція першого порядку, тому що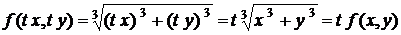 .
.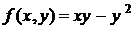 - однорідна функція другого порядку, тому що
- однорідна функція другого порядку, тому що .
. - однорідна функція нульового порядку, тому що
- однорідна функція нульового порядку, тому що .
. називається однорідним, якщо функції при
називається однорідним, якщо функції при  і
і  є однорідними однакового порядку.
є однорідними однакового порядку. і за допомогою заміни змінних
і за допомогою заміни змінних 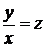 , де
, де  ,
,  , або
, або  зводиться до рівняння із змінними, які розділяються.
зводиться до рівняння із змінними, які розділяються. ,
,  .
.



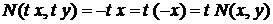
 - однорідні функції першого порядку
- однорідні функції першого порядку
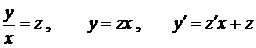
 ,
,  ,
,  ,
,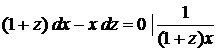
 ,
,  ,
,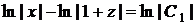 ,
, ,
, 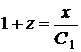 ,
,  ,
,  ,
, - загальний розв'язок.
- загальний розв'язок. ,
,  .
. - розв'язок задачі Коші.
- розв'язок задачі Коші.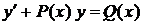 , (17.1)
, (17.1) і
і  - задані неперервні функції від х (або сталі).
- задані неперервні функції від х (або сталі). , то рівняння називається однорідним.
, то рівняння називається однорідним. , (17.2)
, (17.2) . (17.3)
. (17.3)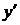 в (17.1), маємо:
в (17.1), маємо: ,
, . (17.4)
. (17.4) такою, щоб
такою, щоб , (17.5)
, (17.5) ,
,  ,
,  ,
,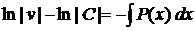 ,
,  ,
,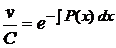 ,
,  .
. візьмемо
візьмемо  .
. ,
,  ,
,  ,
,  .
. й
й  ,
, . (17.6)
. (17.6) ,
, 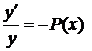 ,
,  ,
, ,
, 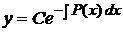 .
. .
. ,
, 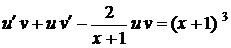 ,
,  .
. , тоді
, тоді ,
,  ,
, .
. ,
,  ,
,  ,
,  ,
, .
. й
й  .
.