
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Властивості визначеного інтегралаВизначений інтеграл має ті ж властивості, що й невизначений. Крім того: 1о. Якщо відрізок інтегрування [a, b] розбитий на дві частини [a, с] і [с, b], то 2о. 3о. 4о. Заміна змінної у визначеному інтегралі
Має місце наступна формула заміни змінної у визначеному інтегралі
Приклад. Обчислити визначені інтеграли: а)
б)
Інтегрування частинами у визначеному інтегралі Застосувавши формулу Ньютона-Лейбница до формули інтегрування частинами, маємо
Приклад. Обчислити визначений інтеграл: 14.6. Обчислення площ плоских фігур за допомогою визначеного інтеграла
Розв'язок.
Приклад. Обчислити площу області, обмеженої лініями Розв'язок.
Інтеграли з нескінченними межами (невласні інтеграли I роду) Нехай функція Означення. Якщо існує скінченна границя  Отже, по означенню маємо: Говорять, що в цьому випадку невласний інтеграл Легко з'ясувати геометричний зміст невласного інтеграла у випадку, коли Аналогічним образом означаються невласні інтеграли і від інших нескінченних інтервалів.
Останню рівність варто розуміти так: якщо кожний із невласних інтегралів, який стоїть справа, існує, то існує (збігається) по означенню й інтеграл, який стоїть зліва. Приклад. Обчислити невласні інтеграли: а) б) Другий інтеграл дорівнює
Отже, Приклад. Показати, для яких значень Розв'язок. При Отже, щодо аналізованого інтеграла можна зробити такі висновки: якщо якщо При |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 323. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. .
. , якщо
, якщо 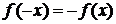 .
.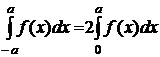 , якщо
, якщо  .
. ,
,  ,
,  .
.


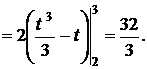

 (3)
(3)
 Якщо на [a, b] функції
Якщо на [a, b] функції 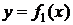 і
і  неперервні, то площа області, обмеженої знизу графіком функції
неперервні, то площа області, обмеженої знизу графіком функції 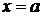 , справа - прямою
, справа - прямою 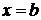 обчислюється за формулою:
обчислюється за формулою:
 Якщо на [a, b] функції
Якщо на [a, b] функції 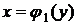 і
і  неперервні, то площа області, обмеженої зліва графіком функції
неперервні, то площа області, обмеженої зліва графіком функції 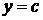 , зверху - прямою
, зверху - прямою 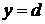 обчислюється за формулою:
обчислюється за формулою:
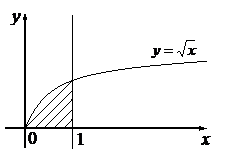 Приклад. Обчислити площу області, обмеженої лініями
Приклад. Обчислити площу області, обмеженої лініями  ,
, 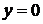 ,
,  .
. (кв. од.)
(кв. од.)
 ,
, 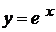 , віссю ординат і прямою
, віссю ординат і прямою 

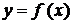 визначена і неперервна при усіх значеннях х таких, що
визначена і неперервна при усіх значеннях х таких, що  . Розглянемо інтеграл
. Розглянемо інтеграл 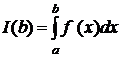 . Цей інтеграл має смисл при усіх
. Цей інтеграл має смисл при усіх  . При зміні b інтеграл змінюється. Розглянемо питання про поведінку цього інтеграла при
. При зміні b інтеграл змінюється. Розглянемо питання про поведінку цього інтеграла при  .
. , то ця границя називається невласним інтегралом від функції
, то ця границя називається невласним інтегралом від функції  і позначається так:
і позначається так: 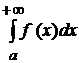 .
. .
. : якщо інтеграл
: якщо інтеграл 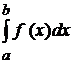 виражає площу області, обмеженої кривою
виражає площу області, обмеженої кривою 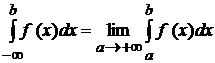 .
.  .
.
 .
. . Обчислимо перший інтеграл.
. Обчислимо перший інтеграл.
 .
.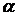 інтеграл
інтеграл 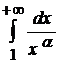 збіжний, а для яких розбіжний.
збіжний, а для яких розбіжний.
 .
.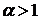 , то
, то  , тобто інтеграл збігається;
, тобто інтеграл збігається;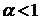 , то
, то  , тобто інтеграл розбігається.
, тобто інтеграл розбігається.
 , тобто інтеграл розбігається.
, тобто інтеграл розбігається.